题目内容
(本小题满分12分)
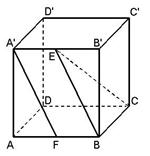
如图，在棱长为2的正方体
中，
分别是
和
的中点，求异面直线
与
所成角的正切值.
(本小题满分12分)
已知圆C：
，直线
：
(I)证明:不论m取什么实数,直线与圆恒交于两点；
(II)求直线被圆截得的弦长最小时的方程,并求此时的弦长.
解：(I) 直线的方程可化为：
…………1分
∴
…………2分
解得
…………3分
即直线恒过定点
…………4分
圆心C
，半径为5，
∴点在圆C内， …………5分
∴直线与圆恒交于两点 …………6分
(II)当
时，弦长最小 …………8分
由
…………9分
得
…………10分
∴直线的方程为
即
…………12分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
