Question

已知数列{a_n}的前n项和S_n满足：log₅(S_n+2)=n(n∈N^*)，求出数列{a_n}的通项公式并判断{a_n}是何种数列.

Answer 1

思路分析：从S_n求出a_n，注意n=1，n≥2分类讨论.再用定义判断是否是等比数列.

解:由log₅(S_n+2)=nS_n=5ⁿ-2,                      ①

当n≥2时，S_n-1=5^n-1-2,                                  ②

①-②，结合S_n-S_n-1=a_n得

a_n=5ⁿ-5^n-1=4·5^n-1(n≥2),

对log₅(S_n+2)=n,令n=1得S₁+2=5，

即a₁=5-2=3,不满足a_n的表达式,

∴a_n=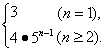

∴数列{a_n}不是等比数列.