题目内容
【题目】已知一列非零向量![]() 满足:
满足:![]() ,
,![]() ,其中
,其中![]() 是正数
是正数
(1)求数列![]() 的通项公式;
的通项公式;
(2)求证:当![]() 时,向量
时,向量![]() 与
与![]() 的夹角为定值;
的夹角为定值;
(3)当![]() 时,把
时,把![]() 中所有与
中所有与![]() 共线的向量按原来的顺序排成一列,记为
共线的向量按原来的顺序排成一列,记为![]() ,令
,令![]() ,
,![]() 为坐标原点,求点列
为坐标原点,求点列![]() 的极限点
的极限点![]() 的坐标.(注:若点坐标为
的坐标.(注:若点坐标为![]() ,且
,且![]() ,则称点
,则称点![]() 为点列的极限点)
为点列的极限点)
【答案】(1)![]() ;(2)定值
;(2)定值![]() ;见解析 (3)
;见解析 (3)![]()
【解析】
(1)根据向量的模长公式得到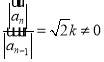 ,由已知可得
,由已知可得![]() ,进而求得
,进而求得![]() 的通项公式;
的通项公式;
(2)利用数量积求解夹角即可证明;
(3)由(2)可知![]() ,即每隔3个向量的两个向量共线,且方向相反,则
,即每隔3个向量的两个向量共线,且方向相反,则![]() ,所以
,所以![]() ,整理可得
,整理可得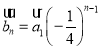 ,将
,将![]() 的坐标代回分别求解
的坐标代回分别求解![]() ,
,![]() ,进而求得极限即可
,进而求得极限即可
(1)由题,![]() 为正数,
为正数,
![]()
所以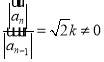 ,
,
因为![]() ,
,
则![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
所以![]()
(2)证明:因为当![]() 时,
时,![]() ,
,
所以![]() ,
,
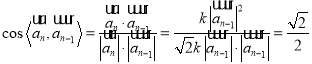 ,
,
则夹角为![]() 是定值
是定值
(3)由(2)可知![]() ,
,
所以每隔3个向量的两个向量共线,且方向相反,
所以与向量![]() 共线的向量为:
共线的向量为:![]() ,
,
记![]() 的单位向量为
的单位向量为![]() ,则
,则![]() ,
,
则![]() ,
,
所以当![]() 时,
时,
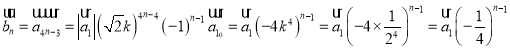
设![]() ,
,
则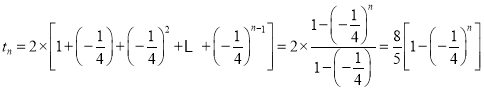 ,
,
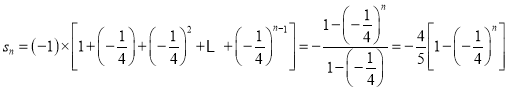 ,
,
则![]() ,
,![]() ,
,
所以点列![]() 的极限点
的极限点![]() 的坐标为
的坐标为![]()

练习册系列答案
相关题目