题目内容
定义在R上的函数y=f(x),满足f(3-x)=f(x),(x-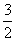 )f′(x)<0,若x1<x2,且x1+x2>3,则有
)f′(x)<0,若x1<x2,且x1+x2>3,则有
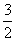 )f′(x)<0,若x1<x2,且x1+x2>3,则有
)f′(x)<0,若x1<x2,且x1+x2>3,则有 [ ]
A.f(x1)<f(x2)
B.f(x1)>f(x2)
C.f(x1)=f(x2)
D.不确定
B

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
题目内容
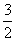 )f′(x)<0,若x1<x2,且x1+x2>3,则有
)f′(x)<0,若x1<x2,且x1+x2>3,则有 [ ]
A.f(x1)<f(x2)
B.f(x1)>f(x2)
C.f(x1)=f(x2)
D.不确定

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案