题目内容
已知函数f(x)=(bx+c)lnx在x=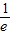 处取得极值,且在x=1处的切线的斜率为1.
处取得极值,且在x=1处的切线的斜率为1.(Ⅰ)求b,c的值及f(x)的单调减区间;
(Ⅱ)设p>0,q>0,g(x)=f(x)+x2,求证:5g(
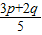 )≤3g(p)+2g(q).
)≤3g(p)+2g(q).
【答案】分析:(Ⅰ)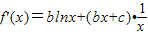 ,
,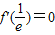 ,故
,故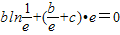 ,由此能求出b,c的值及f(x)的单调减区间.
,由此能求出b,c的值及f(x)的单调减区间.
(Ⅱ)先证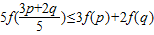 ,即证
,即证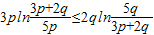 ,再证明5g(
,再证明5g(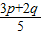 )≤3g(p)+2g(q).
)≤3g(p)+2g(q).
解答:解:(Ⅰ)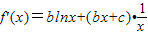 ,(1分)
,(1分)
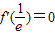 ,
,
∴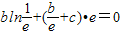 ,
,
即-b+b+ec=0,
∴c=0,
∴f'(x)=blnx+b,
又f'(1)=1,
∴bln1+b=1,
∴b=1,
综上,b=1,c=0,(3分)
f(x)=xlnx,由定义域知x>0,f'(x)=lnx+1,
∵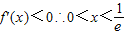 ,
,
∴f(x)的单调减区间为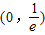 .(5分)
.(5分)
(Ⅱ)先证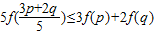
即证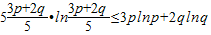
即证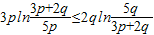 ,(6分)
,(6分)
令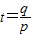 ,∵p>0,q>0,∴t>0,
,∵p>0,q>0,∴t>0,
即证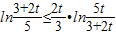
令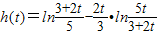 ,
,
则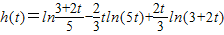 ,
,
∴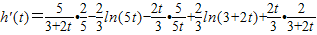 =
=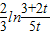 ,(8分)
,(8分)
①当3+2t>5t即0<t<1时,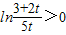 ,即h'(t)>0
,即h'(t)>0
h(t)在(0,1)上递增,∴h(t)<h(1)=0,(9分)
②当3+2t<5t,即t>1时,ln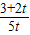 <0,即h′(t)<0,
<0,即h′(t)<0,
h(t)在(1,+∞)上递减,
∴h(t)<h(1)=0,(10分)
③当3+2t=5t,即t=1时,h(t)=h(1)=0,
综合①②③知h(t)≤0,
即ln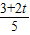 ≤
≤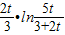 ,(11分)
,(11分)
即5f(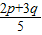 )≤3f(p)+2f(q),
)≤3f(p)+2f(q),
∵5•(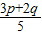 )2-(3p2+2q2)=
)2-(3p2+2q2)=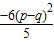 ≤0,
≤0,
∴5•(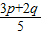 )2≤3p2+2q2,
)2≤3p2+2q2,
综上,得5g(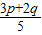 )≤3g(p)+2g(q).(12分)
)≤3g(p)+2g(q).(12分)
点评:本题考查函数的减区间的求法,考查不等式的证明,考查等价转化思想,考查运算推导能力,解题时要认真审题,仔细解答,注意导数性质的灵活运用.
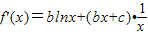 ,
,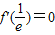 ,故
,故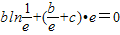 ,由此能求出b,c的值及f(x)的单调减区间.
,由此能求出b,c的值及f(x)的单调减区间.(Ⅱ)先证
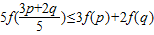 ,即证
,即证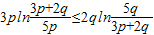 ,再证明5g(
,再证明5g(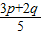 )≤3g(p)+2g(q).
)≤3g(p)+2g(q).解答:解:(Ⅰ)
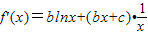 ,(1分)
,(1分)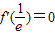 ,
,∴
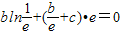 ,
,即-b+b+ec=0,
∴c=0,
∴f'(x)=blnx+b,
又f'(1)=1,
∴bln1+b=1,
∴b=1,
综上,b=1,c=0,(3分)
f(x)=xlnx,由定义域知x>0,f'(x)=lnx+1,
∵
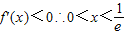 ,
,∴f(x)的单调减区间为
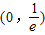 .(5分)
.(5分)(Ⅱ)先证
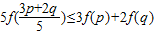
即证
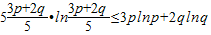
即证
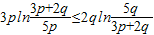 ,(6分)
,(6分)令
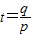 ,∵p>0,q>0,∴t>0,
,∵p>0,q>0,∴t>0,即证
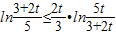
令
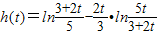 ,
,则
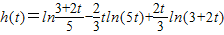 ,
,∴
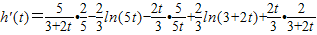 =
=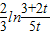 ,(8分)
,(8分)①当3+2t>5t即0<t<1时,
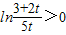 ,即h'(t)>0
,即h'(t)>0h(t)在(0,1)上递增,∴h(t)<h(1)=0,(9分)
②当3+2t<5t,即t>1时,ln
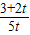 <0,即h′(t)<0,
<0,即h′(t)<0,h(t)在(1,+∞)上递减,
∴h(t)<h(1)=0,(10分)
③当3+2t=5t,即t=1时,h(t)=h(1)=0,
综合①②③知h(t)≤0,
即ln
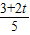 ≤
≤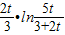 ,(11分)
,(11分)即5f(
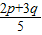 )≤3f(p)+2f(q),
)≤3f(p)+2f(q),∵5•(
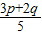 )2-(3p2+2q2)=
)2-(3p2+2q2)=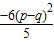 ≤0,
≤0,∴5•(
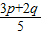 )2≤3p2+2q2,
)2≤3p2+2q2,综上,得5g(
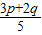 )≤3g(p)+2g(q).(12分)
)≤3g(p)+2g(q).(12分)点评:本题考查函数的减区间的求法,考查不等式的证明,考查等价转化思想,考查运算推导能力,解题时要认真审题,仔细解答,注意导数性质的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|