题目内容
求下列函数的导数.(1)y=ln(sin2x+x3+3);
(2)y=loga(![]() +
+![]() );
);
(3)y=x2ln(x+1);
(4)y=(3x-1)log2(5x+6);
(5)y=ln![]() .
.
分析:对于比较复杂的函数求导,除了利用对数函数求导公式之外,还需要考虑应用复合函数的求导法则来进行.求导过程中,可以先适当进行化简,将对数函数的真数转化为有理函数的形式后再求导数.
解:(1)y′=![]() (sin2x+x3+3)′
(sin2x+x3+3)′
=![]() (2sinxcosx+3x2)
(2sinxcosx+3x2)
=![]() .
.
(2)y′=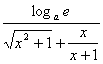 (
(![]() +
+![]() )′
)′
=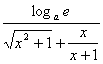 [
[![]() (x2+1)
(x2+1)![]() ·2x+
·2x+![]() ]
]
=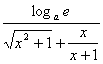 [
[![]() +
+![]() ].
].
(3)y′=2xln(x+1)+![]() (x+1)′
(x+1)′
=2xln(x+1)+![]() .
.
(4)y′=3log2(5x+6)+(3x-1)·![]() ·(5x+6)′log2e
·(5x+6)′log2e
=3log2(5x+6)+![]() .
.
(5)∵y=ln![]()
=![]() ln(1+x2)-
ln(1+x2)-![]() ln(1-x2),
ln(1-x2),
∴y′=![]() -
-![]()
=![]() +
+![]() =
=![]() .
.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目