题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)证明:![]() 在区间
在区间![]() 上单调递增;
上单调递增;
(2)若存在![]() ,使得
,使得![]() 与
与![]() 在
在![]() 的值域相同,求实数
的值域相同,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)求出![]() ,可证明
,可证明![]() ,
,![]() 恒成立,故可得
恒成立,故可得![]() 为
为![]() 上的增函数.
上的增函数.
(2)先讨论![]() 时的情形,此时可把
时的情形,此时可把![]() 的存在性问题转化为
的存在性问题转化为![]() 在
在![]() 存在两个不同的零点问题,利用导数和零点存在定理可得
存在两个不同的零点问题,利用导数和零点存在定理可得![]() .再讨论
.再讨论![]() 的情形,利用两个函数的函数值的符号可判定这种情况不成立,两者结合可求
的情形,利用两个函数的函数值的符号可判定这种情况不成立,两者结合可求![]() 的取值范围.
的取值范围.
(1)因为![]() ,故
,故![]() 且
且![]() ,
,
令![]() ,故
,故![]() .
.
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上为增函数,
上为增函数,
所以![]() ,
,
故![]() ,
,![]() ,故
,故![]() 为
为![]() 上的增函数.
上的增函数.
(2)因为![]() ,故
,故![]() 在
在![]() 为增函数,
为增函数,
故![]() 在
在![]() 上的值域为
上的值域为![]() .
.
当![]() 时,
时,![]() 的值域为
的值域为![]() ,故
,故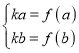 ,
,
所以![]() 在
在![]() 有两个不同的解
有两个不同的解![]() .
.
令![]() ,
,
故![]() 在
在![]() 有两个不同的零点.
有两个不同的零点.
又![]() ,
,
当![]() 时,
时,![]() ,
,
故![]() 为
为![]() 上的单调增函数,
上的单调增函数,
故![]() 在
在![]() 最多有一个解,舍去.
最多有一个解,舍去.
当![]() 时,
时,![]() .
.
取![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
故![]() 在
在![]() 为增函数,
为增函数,
故![]() ,
,
故![]() 在
在![]() 有且只有一个实数解
有且只有一个实数解![]() 且
且![]() .
.
当![]() ,
,![]() ,故
,故![]() 在
在![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 为增函数;
为增函数;
故![]() .
.
又![]() ,所以
,所以![]()
因为![]() 在
在![]() 有两个不同的零点,
有两个不同的零点,
故![]() 即
即![]() .
.
令![]() ,其中
,其中![]() ,
,
故![]() ,故
,故![]() 在
在![]() 上为减函数,
上为减函数,
故不等式![]() 的解为
的解为![]() ,
,
所以![]() .
.
令![]() 及
及![]() ,
,
因为![]() 为开口向上的二次函数,
为开口向上的二次函数,
故存在![]() ,使得当任意
,使得当任意![]() 时,总有
时,总有![]() ,
,
而![]() ,故
,故![]() 在
在![]() 上为增函数,
上为增函数,
当对任意的![]() 时,总有
时,总有![]() ,
,
因为![]() ,故当
,故当![]() ,
,![]() ,
,
根据零点存在定理,![]() 在
在![]() 上有且只有一个零点.
上有且只有一个零点.
因为![]() 在
在![]() 有两个不同的零点,故
有两个不同的零点,故![]() ,
,
所以![]() 即
即![]() ,
,
又![]() ,故
,故![]() ,
,
所以![]() .
.
当![]() 时,
时,![]() 在
在![]() 上始终满足
上始终满足![]() ,
,
由(1)可知![]() 在
在![]() 为增函数,故
为增函数,故![]() ,
,
不符合题设要求,舍去.
综上,![]() .
.

【题目】如图是某小区2017年1月至2018年1月当月在售二手房均价(单位:万元/平方米)的散点图.(图中月份代码1—13分别对应2017年1月—2018年1月)
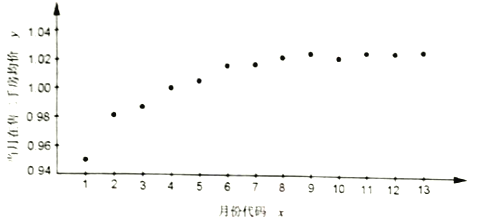
由散点图选择![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程分别为
两个模型进行拟合,经过数据处理得到两个回归方程分别为![]() 和
和![]() ,并得到以下一些统计量的值:
,并得到以下一些统计量的值:
|
| |
残差平方和 | 0.000591 | 0.000164 |
总偏差平方和 | 0.006050 | |
(1)请利用相关指数![]() 判断哪个模型的拟合效果更好;
判断哪个模型的拟合效果更好;
(2)某位购房者拟于2018年6月份购买这个小区![]() 平方米的二手房(欲
平方米的二手房(欲
购房为其家庭首套房).若购房时该小区所有住房的房产证均已满2年但未满5年,请你利用(1)中拟合效果更好的模型估算该购房者应支付的购房金额.(购房金额=房款+税费;房屋均价精确到0.001万元/平方米)
附注:根据有关规定,二手房交易需要缴纳若干项税费,税费是按房屋的计税价格进行征收.(计税价格=房款),征收方式见下表:
契税 (买方缴纳) | 首套面积90平方米以内(含90平方米)为1%;首套面积90平方米以上且144平方米以内(含144平方米)为1.5%;面积144平方米以上或非首套为3% |
增值税 (卖方缴纳) | 房产证未满2年或满2年且面积在144平方米以上(不含144平方米)为5.6%;其他情况免征 |
个人所得税 (卖方缴纳) | 首套面积144平方米以内(含144平方米)为1%;面积144平方米以上或非首套均为1.5%;房产证满5年且是家庭唯一住房的免征 |
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() . 参考公式:相关指数
. 参考公式:相关指数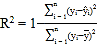 .
.