题目内容
数列{an}中,已知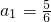 ,
,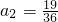 ,且
,且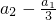 ,
,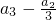 ,…,an+1-
,…,an+1-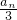 是公比为
是公比为 的等比数列.
的等比数列.
(1)求证数列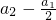 ,
,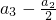 ,…,
,…,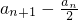 是公比为
是公比为 的等比数列.
的等比数列.
(2)求数列{an}的通项公式.
(3)问是否存在除 ,
, 以外的实数k,使得数列{an+1-kan}成等比数列.
以外的实数k,使得数列{an+1-kan}成等比数列.
解:(1)由题意可得:因为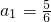 ,
,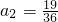 ,
,
所以 ,
,
又因为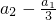 ,
,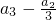 ,…,an+1-
,…,an+1-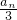 是公比为
是公比为 的等比数列,
的等比数列,
所以
所以
= ,
,
所以数列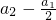 ,
,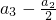 ,…,
,…,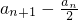 是公比为
是公比为 的等比数列.
的等比数列.
(2)由(1)可得: ,又因为
,又因为 ,
,
所以两式相减得 ,
,
所以 ,
,
所以 .
.
(3)假设存在这样的k,k≠
则有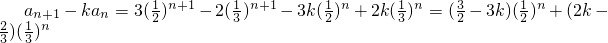
所以 ,
,
即 解得:
解得: ,
,
所以不存在除 ,
, 以外的实数k使得数列{an+1-kan}成等比数列.
以外的实数k使得数列{an+1-kan}成等比数列.
分析:(1)由题意可得:因为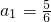 ,
,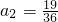 ,所以
,所以 ,根据题意可得:
,根据题意可得: ,进而达到
,进而达到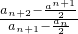 =
= ,即可证明结论.
,即可证明结论.
(2)由(1)可得: ,所以
,所以 .
.
(3)假设存在这样的k,k≠ ,可得
,可得 ,令an+2-kan+1=qan+1-qkan,即
,令an+2-kan+1=qan+1-qkan,即 解得:
解得: ,进而达到答案.
,进而达到答案.
点评:本题主要考查等比数列的性质,以及等比数列的通项公式以及等比数列的判定,此题属于难题.
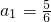 ,
,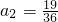 ,
,所以
 ,
,又因为
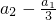 ,
,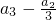 ,…,an+1-
,…,an+1-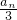 是公比为
是公比为 的等比数列,
的等比数列,所以

所以

=
 ,
,所以数列
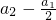 ,
,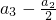 ,…,
,…,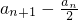 是公比为
是公比为 的等比数列.
的等比数列.(2)由(1)可得:
 ,又因为
,又因为 ,
,所以两式相减得
 ,
,所以
 ,
,所以
 .
.(3)假设存在这样的k,k≠

则有
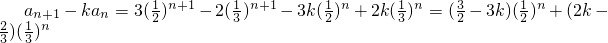
所以
 ,
,即
 解得:
解得: ,
,所以不存在除
 ,
, 以外的实数k使得数列{an+1-kan}成等比数列.
以外的实数k使得数列{an+1-kan}成等比数列.分析:(1)由题意可得:因为
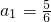 ,
,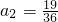 ,所以
,所以 ,根据题意可得:
,根据题意可得: ,进而达到
,进而达到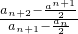 =
= ,即可证明结论.
,即可证明结论.(2)由(1)可得:
 ,所以
,所以 .
.(3)假设存在这样的k,k≠
 ,可得
,可得 ,令an+2-kan+1=qan+1-qkan,即
,令an+2-kan+1=qan+1-qkan,即 解得:
解得: ,进而达到答案.
,进而达到答案.点评:本题主要考查等比数列的性质,以及等比数列的通项公式以及等比数列的判定,此题属于难题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目