题目内容
△ABC中,已知tanA+tanB+
解:∵tanA+tanB=-![]() (1-tanA·tanB),
(1-tanA·tanB),
∴![]() =-
=-![]() ,即tan(A+B)=-
,即tan(A+B)=-![]() .
.
∵0°<A+B<180°,∴A+B=120°.
∴C=60°.
∵![]() absinC=
absinC= ![]() ,∴ab=6. ①
,∴ab=6. ①
∵c2=a2+b2-2abcosC,
∴(![]() )2=a2+b2-ab=(a+b)2-3ab.
)2=a2+b2-ab=(a+b)2-3ab.
∴(a+b)2=![]() .∴a+b=
.∴a+b=![]() . ②
. ②
由①②解得a=![]() ,b=4或a=4,b=
,b=4或a=4,b=![]() .
.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 ;
; (注:
(注: 表示△ABC的面积)
表示△ABC的面积) ;
; (注:
(注: 表示△ABC的面积)
表示△ABC的面积)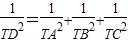 ;
; (注:S△ABC表示△ABC的面积)
(注:S△ABC表示△ABC的面积) ;
; (注:S△ABC表示△ABC的面积)
(注:S△ABC表示△ABC的面积)