题目内容
18.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),M、N为双曲线上关于原点对称的两点,P为双曲线上的点,且直线PM、PN斜率分别为k1、k2,若k1•k2=$\frac{5}{4}$,则双曲线离心率为( )| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
分析 设出点M,点N,点P的坐标,求出斜率,将点M,N的坐标代入方程,两式相减,再结合kPM•kPN=$\frac{5}{4}$,即可求得结论.
解答 解:由题意,设M(x1,y1),P(x2,y2),则N(-x1,-y1)
∴kPM•kPN=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$•$\frac{{y}_{2}+{y}_{1}}{{x}_{2}+{x}_{1}}$=$\frac{{{y}_{2}}^{2}-{{y}_{1}}^{2}}{{{x}_{2}}^{2}-{{x}_{1}}^{2}}$,
∵$\frac{{{x}_{1}}^{2}}{{a}^{2}}-\frac{{{y}_{1}}^{2}}{{b}^{2}}$=1,$\frac{{{x}_{2}}^{2}}{{a}^{2}}$-$\frac{{{y}_{2}}^{2}}{{b}^{2}}$=1,
∴两式相减可得$\frac{{{y}_{2}}^{2}-{{y}_{1}}^{2}}{{{x}_{2}}^{2}-{{x}_{1}}^{2}}$=$\frac{{b}^{2}}{{a}^{2}}$
∵kPM•kPN=$\frac{5}{4}$,
∴$\frac{{b}^{2}}{{a}^{2}}$=$\frac{5}{4}$,
∴b=$\frac{\sqrt{5}}{2}$a,
∴c=$\sqrt{{a}^{2}+{b}^{2}}$=$\frac{3}{2}$a,
∴e=$\frac{c}{a}$=$\frac{3}{2}$.
故选:B.
点评 本题考查双曲线的方程,考查双曲线的几何性质,考查直线的斜率公式和点差法的运用,属于中档题.

练习册系列答案
相关题目
11.函数f(x)=sinx+sin($\frac{2π}{3}$-x)的图象的一条对称轴为( )
| A. | x=$\frac{π}{2}$ | B. | x=π | C. | x=$\frac{π}{6}$ | D. | x=$\frac{π}{3}$ |
10. 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )| A. | 对任意的a,b,存在点E,使得B1D⊥EC1 | |
| B. | 当且仅当a=b时,存在点E,使得B1D⊥EC1 | |
| C. | 当且仅当a≥b时,存在点E,使得B1D⊥EC1 | |
| D. | 当且仅当a≤b时,存在点E,使得B1D⊥EC1 |
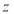 满足
满足 ,则
,则 ( )
( )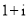 B.
B.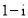
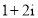 D.
D.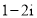

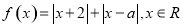 .
.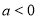 ,且
,且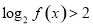 对任意
对任意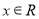 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,且关于
,且关于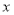 的不等式
的不等式 有解,求实数
有解,求实数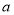 的取值范围.
的取值范围.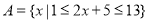 ,
,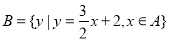 ,则
,则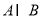 等于( )
等于( )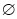 B.
B.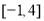
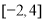 D.
D.