题目内容
设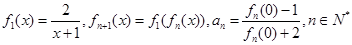
（1）求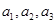
，并求数列
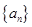的通项公式.
（2）已知函数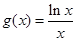
在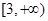
上为减函数，设数列
的前
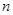的和为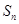
，
求证：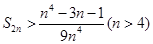
【答案】
（1）
，（2）利用函数的单调性证明不等式
【解析】
试题分析：
3分
是首项为
，公比为
的等比数列，
，……6分
（2）
……9分
,
在
上为减函数，当
时，
……12分
考点：本题考查了数列通项公式的求法及不等式的证明
点评：数列与函数、方程、不等式的综合问题，要注意将其分解为数学分支中的问题来解决
练习册系列答案
相关题目
右表是某班英语及数学成绩的分布表，已知该班有50名学生，成绩分1至5个档次．如：表中所示英语成绩为4分，数学成绩为2分的学生有5人．现设该班任意一位学生的英语成绩为m，数学成绩为n．
（1）求m=4，n=3的概率；
（2）求在m≥3的条件下，n=3的概率；
（3）求a+b的值，并求m的数学期望；
（4）若m=2与n=4是相互独立的，求a，b的值．
| n m |
数 学 | |||||
| 5 | 4 | 3 | 2 | 1 | ||
| 英 语 |
5 | 1 | 3 | 1 | 0 | 1 |
| 4 | 1 | 0 | 7 | 5 | 1 | |
| 3 | 2 | 1 | 0 | 9 | 3 | |
| 2 | 1 | b | 6 | 0 | a | |
| 1 | 0 | 0 | 1 | 1 | 3 | |
（2）求在m≥3的条件下，n=3的概率；
（3）求a+b的值，并求m的数学期望；
（4）若m=2与n=4是相互独立的，求a，b的值．
满足
，则称数列
中，
，点
在函数
的图像上，其中
为正整数。
是“平方递推数列”，且数列
为等比数列。
，即
，求数列
，求数列
的前
，并求使
的
右表是某班英语及数学成绩的分布表，已知该班有50名学生，成绩分1至5个档次．如：表中所示英语成绩为4分，数学成绩为2分的学生有5人．现设该班任意一位学生的英语成绩为m，数学成绩为n．
（1）求m=4，n=3的概率；
（2）求在m≥3的条件下，n=3的概率；
（3）求a+b的值，并求m的数学期望；
（4）若m=2与n=4是相互独立的，求a，b的值．
| n m | 数 学 | |||||
| 5 | 4 | 3 | 2 | 1 | ||
| 英 语 | 5 | 1 | 3 | 1 | 1 | |
| 4 | 1 | 7 | 5 | 1 | ||
| 3 | 2 | 1 | 9 | 3 | ||
| 2 | 1 | b | 6 | a | ||
| 1 | 1 | 1 | 3 | |||
（2）求在m≥3的条件下，n=3的概率；
（3）求a+b的值，并求m的数学期望；
（4）若m=2与n=4是相互独立的，求a，b的值．