题目内容
图△ABC和△BCD都是边长为2的正三角形，且二面角A-BC-D的大小为60°，则AD的长为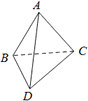
- A.2
- B.
- C.
- D.
C
分析：取BC的中点O，连接OA，OD，确定∠AOD为二面角A-BC-D的平面角，即∠AOD=60°，从而可得结论．
解答：
解：取BC的中点O，连接OA，OD
∵△ABC和△BCD都是边长为2的正三角形
∴AO⊥BC，DO⊥BC，AO=DO=
∴∠AOD为二面角A-BC-D的平面角，即∠AOD=60°
∵AO=DO=
∴AD=
故选C．
点评：本题考查面面角，考查学生的计算能力，确定面面角是关键．
分析：取BC的中点O，连接OA，OD，确定∠AOD为二面角A-BC-D的平面角，即∠AOD=60°，从而可得结论．
解答：
解：取BC的中点O，连接OA，OD∵△ABC和△BCD都是边长为2的正三角形
∴AO⊥BC，DO⊥BC，AO=DO=
∴∠AOD为二面角A-BC-D的平面角，即∠AOD=60°
∵AO=DO=
∴AD=
故选C．
点评：本题考查面面角，考查学生的计算能力，确定面面角是关键．
练习册系列答案
相关题目
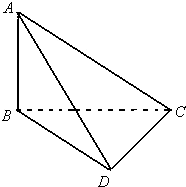如图，已知△ABC和△BCD所在平面互相垂直，∠ABC=∠BCD=90°，AB=a，BC=b，CD=c，且a2+b2+c2=1，则三棱锥A-BCD的外接球的表面积为
