题目内容
设函数f(x)=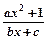 是奇函数(a,b,c都是整数)且f(1)=2,f(2)<3
是奇函数(a,b,c都是整数)且f(1)=2,f(2)<3
(1)求a,b,c的值;
(2)当x<0,f(x)的单调性如何?用单调性定义证明你的结论。
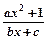 是奇函数(a,b,c都是整数)且f(1)=2,f(2)<3
是奇函数(a,b,c都是整数)且f(1)=2,f(2)<3(1)求a,b,c的值;
(2)当x<0,f(x)的单调性如何?用单调性定义证明你的结论。
解:(Ⅰ)由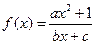 是奇函数,得
是奇函数,得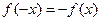 对定义域内x恒成立,
对定义域内x恒成立,
则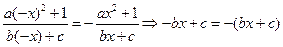 对对定义域内x恒成立,即
对对定义域内x恒成立,即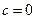
(或由定义域关于原点对称得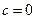 )
)
又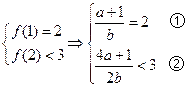 由①得
由①得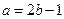 代入②得
代入②得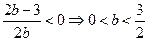 ,
,
又 是整数,得
是整数,得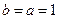
(Ⅱ)由(Ⅰ)知,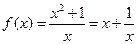 ,当
,当 ,
,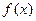 在
在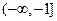 上单调递增,在
上单调递增,在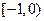
上单调递减.下用定义证明之.
设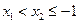 ,则
,则
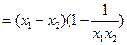 ,因为
,因为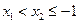 ,
,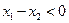 ,
,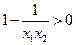
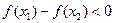 ,故
,故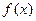 在
在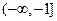 上单调递增;
上单调递增;
同理,可证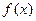 在
在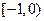 上单调
上单调 递减.
递减.
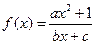 是奇函数,得
是奇函数,得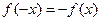 对定义域内x恒成立,
对定义域内x恒成立,则
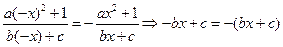 对对定义域内x恒成立,即
对对定义域内x恒成立,即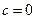
(或由定义域关于原点对称得
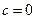 )
)又
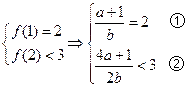 由①得
由①得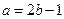 代入②得
代入②得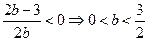 ,
,又
 是整数,得
是整数,得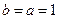
(Ⅱ)由(Ⅰ)知,
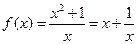 ,当
,当 ,
,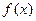 在
在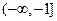 上单调递增,在
上单调递增,在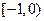
上单调递减.下用定义证明之.
设
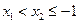 ,则
,则
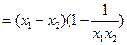 ,因为
,因为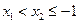 ,
,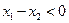 ,
,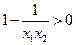
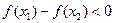 ,故
,故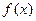 在
在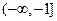 上单调递增;
上单调递增;同理,可证
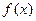 在
在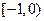 上单调
上单调 递减.
递减.略

练习册系列答案
相关题目
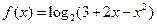 . (1) 求函数
. (1) 求函数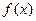 的定义域;(2) 求证
的定义域;(2) 求证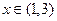 上是减函数;(3) 求函数
上是减函数;(3) 求函数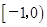 上为减函数的是( )
上为减函数的是( )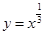
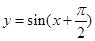
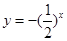
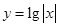
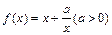 ,
,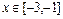 时,
时,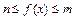 恒成立,若a≥9,求
恒成立,若a≥9,求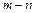 的最小值.
的最小值.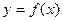 且
且 。
。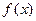 的解析式及定义域。(Ⅱ)求
的解析式及定义域。(Ⅱ)求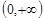 的是
的是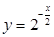
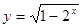
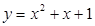
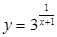
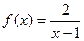 在区间[2,6]上的最大值和最小值.
在区间[2,6]上的最大值和最小值.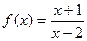 ,
,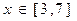
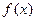 的单调性,并用定义加以证明;(2)求函数
的单调性,并用定义加以证明;(2)求函数