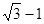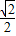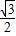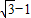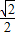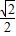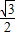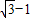题目内容
一个圆的圆心为椭圆的右焦点,且该圆过椭圆的中心交椭圆于P,直线PF1(F1为椭圆的左焦点)是该圆的切线,则椭圆的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:根据题意思可得:点P是切点,所以PF2=c并且PF1⊥PF2.所以∠PF1F2=30°,所以|PF2|=
c.根据椭圆的定义可得|PF1|+|PF2|=2a,
所以|PF2|=2a-c.进而得到答案.
| 3 |
所以|PF2|=2a-c.进而得到答案.
解答:解:设F2为椭圆的右焦点
由题意可得:圆与椭圆交于P,并且直线PF1(F1为椭圆的左焦点)是该圆的切线,
所以点P是切点,所以PF2=c并且PF1⊥PF2.
又因为F1F2=2c,所以∠PF1F2=30°,所以|PF2|=
c.
根据椭圆的定义可得|PF1|+|PF2|=2a,
所以|PF2|=2a-c.
所以2a-c=
c,所以e=
-1.
故选D.
由题意可得:圆与椭圆交于P,并且直线PF1(F1为椭圆的左焦点)是该圆的切线,
所以点P是切点,所以PF2=c并且PF1⊥PF2.
又因为F1F2=2c,所以∠PF1F2=30°,所以|PF2|=
| 3 |
根据椭圆的定义可得|PF1|+|PF2|=2a,
所以|PF2|=2a-c.
所以2a-c=
| 3 |
| 3 |
故选D.
点评:解决此类问题的关键是熟练掌握直线与圆的相切问题,以即椭圆的定义.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 (F
(F B、
B、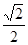 C、
C、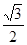 D、
D、