题目内容
知二次函数f(x)满足f(-2+k)=f(-2-k)(k∈R),且该函数的图象与y轴交于点(0,1),在x轴上截得的线段长为2
,求该二次函数解析式为
| 2 |
f(x)=
x2+2x+1
| 1 |
| 2 |
f(x)=
x2+2x+1
.| 1 |
| 2 |
分析:先设出二次函数f(x)=ax2+bx+c(a≠0)的表达式,再利用其对称性、与y轴交于点(0,1)及在x轴上截得的线段长为2
,可列出关于a、b、c一个方程组,解出即可.
| 2 |
解答:解:设二次函数f(x)=ax2+bx+c(a≠0).
∵二次函数f(x)满足f(-2+k)=f(-2-k)(k∈R),可知该二次函数关于直线x=-2对称,∴-
=-2,即b=4a.
∵该函数的图象与y轴交于点(0,1),∴f(0)=1,即c=1.
设二次函数f(x)=ax2+bx+c与x轴相较于点(x1,0),(x2,0).
令f(x)=ax2+bx+c=0,则x1+x2=-
,x1x2=
.
∵此二次函数的图象在x轴上截得的线段长为2
,
∴|x2-x1|=2
,即
=2
.
∴
-4×
=8,即b2-4ac=8a2.
联立
.解得
.
∴f(x)=
x2+2x+1.
∵二次函数f(x)满足f(-2+k)=f(-2-k)(k∈R),可知该二次函数关于直线x=-2对称,∴-
| b |
| 2a |
∵该函数的图象与y轴交于点(0,1),∴f(0)=1,即c=1.
设二次函数f(x)=ax2+bx+c与x轴相较于点(x1,0),(x2,0).
令f(x)=ax2+bx+c=0,则x1+x2=-
| b |
| a |
| c |
| a |
∵此二次函数的图象在x轴上截得的线段长为2
| 2 |
∴|x2-x1|=2
| 2 |
| (x1+x2)2-4x1x2 |
| 2 |
∴
| b2 |
| a2 |
| c |
| a |
联立
|
|
∴f(x)=
| 1 |
| 2 |
点评:熟练掌握二次函数的性质是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
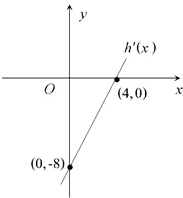 已知二次函数h(x)=ax2+bx+c(其中c<3),其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).
已知二次函数h(x)=ax2+bx+c(其中c<3),其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).