题目内容
14．如图，试描述函数y=f（x）在x=-3，-2，0，1附近的变化情况．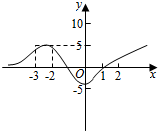
分析 根据导数的几何意义，即可判断x=-3，-2，0，1附近的变化情况．
解答 解：（1）、函数f（x）在x=-3处切线斜率f′（-3）＞0，曲线是上升的．即函数f（x）在x=-3附近是单调递增的，
（2）、函数f（x）在x=-2处切线的斜率f′（-2）＜0，曲线是下降的即函数f（x）在x=-4附近是单调递减的，
（3）、函数f（x）在x=0处切线的斜率f′（0）接近于0，所以函数f（x）在x=0附近几乎没有变化，
（4）、函数f（x）在x=1切线的斜率f′（1 ）＞0，曲线是上升的．即函数f（x）在x=1附近是单调递增的．
点评 本题考查了导数的几何意义，属于基础题．
练习册系列答案
相关题目
5．“?n∈N*，a${\;}_{n+1}^{2}$=anan+2”是“数列{an}为等比数列”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
2．设函数f（x）是定义在R上的函数，则“x0是函数f（x）的极值点”是“f′（x0）=0”的（ ）条件．
| A． | 充分不必要 | B． | 必要不充分 | ||
| C． | 充要 | D． | 既不充分也不必要 |
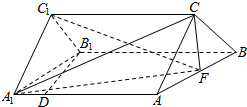已知三棱柱ABC-A1B1C1中，AA1⊥平面ABC，△ABC为边长为1的正三角形，且AA1=2，D为AA1上的点，且A1D=$\frac{1}{4}$，F为AB的中点．
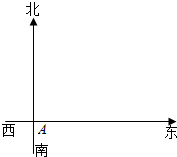一辆消防车从A地去B地执行任务．先从A地向北偏东30°方向行驶2千米到D地．然后从D地沿北偏东60°方向行驶6千米到达C地，从C地又向南偏西30°方向行驶2千米才到达B地．