Question

如下图,圆锥和一个球面相交,球心在圆锥的顶点,球半径等于圆锥的高，若圆锥的侧面被球与圆锥的交线所平分,求圆锥的高与母线间夹角α的大小.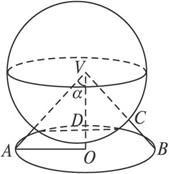

Answer 1

思路解析：首先求出圆锥的高和母线之间的关系,在三角形中即可求出高与母线的夹角的一个三角函数值.

解：△VAB是轴截面,设VB交⊙V于C,作CD⊥VO于D,记VO=h.

由已知∠AVO=α=∠BVO,

∵VO＝h＝VBcosα,∴VB=.

又BO=htanα,CD＝VCsinα＝VOsinα＝hsinα.

根据题意，小锥侧面积是大锥侧面积的一半，可列出方程

π·CD·VC=π·BO·VB,

即hsinα·h=h·tanα·.

化简,得cos²α=,cosα=±.

根据实际情况，cosα=,所以α=45°.