题目内容
在四边形ABCD中,“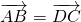 ,且
,且 ”是“四边形ABCD是菱形”的
”是“四边形ABCD是菱形”的
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既不充分也不必要条件
C
分析:根据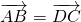 ,以及共线向量定理可得AB∥CD,且AB=CD,从而可知在四边形ABCD是平行四边形,又由
,以及共线向量定理可得AB∥CD,且AB=CD,从而可知在四边形ABCD是平行四边形,又由 ,得四边形ABCD的对角线互相垂直,因此得到四边形ABCD为菱形.反之也成立.再根据充要条件进行判断即得.
,得四边形ABCD的对角线互相垂直,因此得到四边形ABCD为菱形.反之也成立.再根据充要条件进行判断即得.
解答:由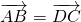 可得四边形ABCD是平行四边形,
可得四边形ABCD是平行四边形,
由 得四边形ABCD的对角线互相垂直,
得四边形ABCD的对角线互相垂直,
∴对角线互相垂直的平行四边形是菱形.
反之也成立.
∴“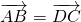 ,且
,且 ”是“四边形ABCD是菱形”的充要条件.
”是“四边形ABCD是菱形”的充要条件.
故选C.
点评:此题是个基础题.考查必要条件、充分条件与充要条件的判断、共线向量定理以及向量在几何中的应用,考查学生利用知识分析解决问题的能力.
分析:根据
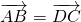 ,以及共线向量定理可得AB∥CD,且AB=CD,从而可知在四边形ABCD是平行四边形,又由
,以及共线向量定理可得AB∥CD,且AB=CD,从而可知在四边形ABCD是平行四边形,又由 ,得四边形ABCD的对角线互相垂直,因此得到四边形ABCD为菱形.反之也成立.再根据充要条件进行判断即得.
,得四边形ABCD的对角线互相垂直,因此得到四边形ABCD为菱形.反之也成立.再根据充要条件进行判断即得.解答:由
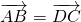 可得四边形ABCD是平行四边形,
可得四边形ABCD是平行四边形,由
 得四边形ABCD的对角线互相垂直,
得四边形ABCD的对角线互相垂直,∴对角线互相垂直的平行四边形是菱形.
反之也成立.
∴“
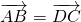 ,且
,且 ”是“四边形ABCD是菱形”的充要条件.
”是“四边形ABCD是菱形”的充要条件.故选C.
点评:此题是个基础题.考查必要条件、充分条件与充要条件的判断、共线向量定理以及向量在几何中的应用,考查学生利用知识分析解决问题的能力.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 如图所示,在四边形ABCD中,EF∥BC,FG∥AD,则
如图所示,在四边形ABCD中,EF∥BC,FG∥AD,则