题目内容
(本小题满分15分)已知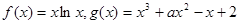 .
.
(1)如果函数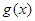 的单调递减区间为
的单调递减区间为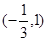 ,求函数
,求函数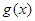 的解析式;
的解析式;
(2)在(Ⅰ)的条件下,求函数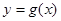 的图像在点
的图像在点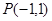 处的切线方程;
处的切线方程;
(3)若不等式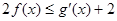 恒成立,求实数
恒成立,求实数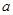 的取值范围.
的取值范围.
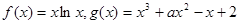 .
.(1)如果函数
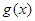 的单调递减区间为
的单调递减区间为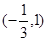 ,求函数
,求函数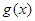 的解析式;
的解析式;(2)在(Ⅰ)的条件下,求函数
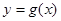 的图像在点
的图像在点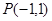 处的切线方程;
处的切线方程;(3)若不等式
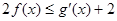 恒成立,求实数
恒成立,求实数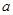 的取值范围.
的取值范围. (1) 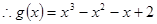 . (2)
. (2) 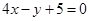 . (3)
. (3) 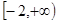 .
.
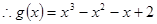 . (2)
. (2) 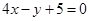 . (3)
. (3) 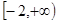 .
. 解决不等式恒成立问题,常用的方法是分离出参数,构造新函数,求出新函数的最值,得到参数的范围.
(I)求出g(x)的导函数,令导函数小于0得到不等式的解集,得到相应方程的两个根,将根代入,求出a的值.
(II)求出g(x)的导数在x=-1的值即曲线的切线斜率,利用点斜式求出切线的方程
(III)求出不等式,分离出参数A,构造函数h(x),利用导数求出h(x)的最大值,令a大于等于最大值,求出a的范围.
解:(1)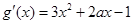 ………………………1分
………………………1分
由题意 的解集是
的解集是 即
即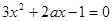 的两根分别是
的两根分别是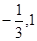 .
.
将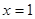 或
或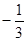 代入方程
代入方程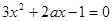 得
得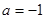 .
. 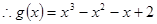 . …………4分
. …………4分
(2)由(Ⅰ)知: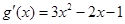 ,
,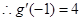 ,
,
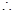 点
点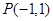 处的切线斜率
处的切线斜率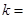
 ,
,
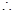 函数y=
函数y=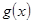 的图像在点
的图像在点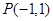 处的切线方程为:
处的切线方程为: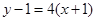 ,即
,即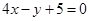 . …………7分
. …………7分
(3)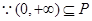 ,
,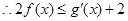 即:
即: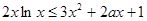 对
对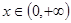 上恒成立
上恒成立
可得 对
对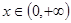 上恒成立……9分
上恒成立……9分
设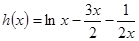 , 则
, 则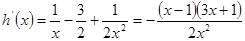
令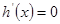 ,得
,得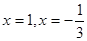 (舍)
(舍)
当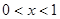 时,
时,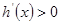 ;当
;当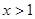 时,
时, 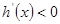 ………..12
………..12
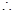 当
当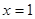 时,
时,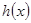 取得最大值,
取得最大值, 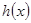
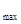 =-2
=-2  .
.
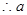 的取值范围是
的取值范围是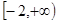 . ………15分
. ………15分
(I)求出g(x)的导函数,令导函数小于0得到不等式的解集,得到相应方程的两个根,将根代入,求出a的值.
(II)求出g(x)的导数在x=-1的值即曲线的切线斜率,利用点斜式求出切线的方程
(III)求出不等式,分离出参数A,构造函数h(x),利用导数求出h(x)的最大值,令a大于等于最大值,求出a的范围.
解:(1)
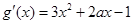 ………………………1分
………………………1分由题意
 的解集是
的解集是 即
即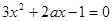 的两根分别是
的两根分别是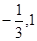 .
.将
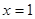 或
或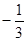 代入方程
代入方程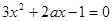 得
得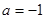 .
. 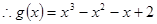 . …………4分
. …………4分(2)由(Ⅰ)知:
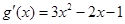 ,
,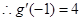 ,
,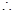 点
点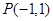 处的切线斜率
处的切线斜率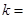
 ,
, 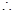 函数y=
函数y=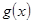 的图像在点
的图像在点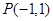 处的切线方程为:
处的切线方程为: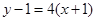 ,即
,即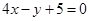 . …………7分
. …………7分(3)
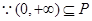 ,
,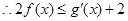 即:
即: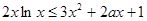 对
对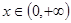 上恒成立
上恒成立 可得
 对
对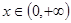 上恒成立……9分
上恒成立……9分设
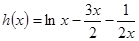 , 则
, 则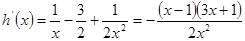
令
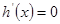 ,得
,得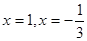 (舍)
(舍)当
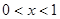 时,
时,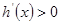 ;当
;当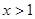 时,
时, 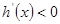 ………..12
………..12 当
当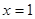 时,
时,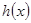 取得最大值,
取得最大值, 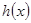
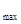 =-2
=-2  .
.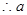 的取值范围是
的取值范围是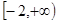 . ………15分
. ………15分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
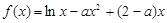 .
.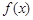 的单调性;
的单调性;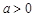 ,证明:当
,证明:当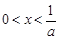 时,
时,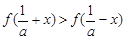 ;
;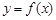 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明: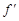 (x0)<0.(本题满分14分)
(x0)<0.(本题满分14分) (a≠0)
(a≠0)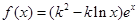 (
(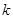 为非零常数,
为非零常数,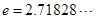 是自然对数的底数),曲线
是自然对数的底数),曲线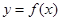 在点
在点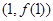 处的切线与
处的切线与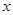 轴平行.
轴平行.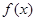 的单调性;
的单调性;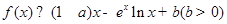 , 求
, 求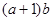 的最大值.
的最大值.  函数
函数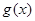 的图象与
的图象与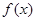 的图象关于直线
的图象关于直线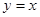 对称,
对称,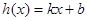 .
.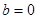 时,若对
时,若对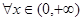 均有
均有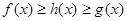 成立,求实数
成立,求实数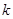 的取值范围;
的取值范围;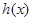 的图象与
的图象与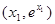 和
和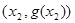 ,其中
,其中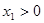 .
.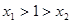 ;
;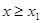 时,关于
时,关于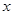 的不等式
的不等式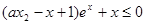 恒成立,求实数
恒成立,求实数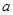 的取值范围.
的取值范围.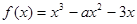 .
.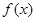 在
在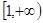 上是增函数,求实数
上是增函数,求实数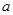 的取值范围;
的取值范围;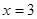 是
是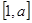 上的最小值和最大值.
上的最小值和最大值. ,当
,当 时取极小值
时取极小值 。
。 的解析式;
的解析式; 与曲线
与曲线 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数 的取值范围。
的取值范围。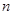 ,设曲线
,设曲线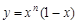 在
在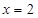 处的切线与
处的切线与 轴交点的纵坐标为
轴交点的纵坐标为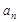 ,
,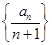 的前
的前 ,则曲线
,则曲线 在点
在点 处的切线的斜率为
处的切线的斜率为