题目内容
平面α与平面β相交成一个锐二面角θ,平面α上的一个圆在平面β上的射影是一个离心率为 的椭圆,则θ等于
的椭圆,则θ等于
- A.30°
- B.45°
- C.60°
- D.75°
A
分析:根据题意,设圆的半径为r,由题意可得b=r,根据离心率与a,b,c的关系可得a= r,所以cosθ=
r,所以cosθ= =
= ,所以θ=30°.
,所以θ=30°.
解答:由题意可得:平面α上的一个圆在平面β上的射影是一个离心率为 的椭圆,也可以说为:β上的一个离心率为
的椭圆,也可以说为:β上的一个离心率为  的椭圆在α上的射影是一个圆,
的椭圆在α上的射影是一个圆,
设圆的半径为r,所以b=r,
又因为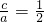 ,并且b2=a2-c2,所以a=
,并且b2=a2-c2,所以a= r.
r.
所以cosθ= =
= ,所以θ=30°.
,所以θ=30°.
故选A.
点评:本题以二面角为载体,考查与二面角有关的立体几何综合题,以及椭圆的性质,是解析几何与立体几何结合的一道综合题.
分析:根据题意,设圆的半径为r,由题意可得b=r,根据离心率与a,b,c的关系可得a=
 r,所以cosθ=
r,所以cosθ= =
= ,所以θ=30°.
,所以θ=30°.解答:由题意可得:平面α上的一个圆在平面β上的射影是一个离心率为
 的椭圆,也可以说为:β上的一个离心率为
的椭圆,也可以说为:β上的一个离心率为  的椭圆在α上的射影是一个圆,
的椭圆在α上的射影是一个圆,设圆的半径为r,所以b=r,
又因为
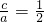 ,并且b2=a2-c2,所以a=
,并且b2=a2-c2,所以a= r.
r.所以cosθ=
 =
= ,所以θ=30°.
,所以θ=30°.故选A.
点评:本题以二面角为载体,考查与二面角有关的立体几何综合题,以及椭圆的性质,是解析几何与立体几何结合的一道综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,平面α与平面β相交成锐角θ,平面α内的一个圆在平面β上的射影是离心率为
如图,平面α与平面β相交成锐角θ,平面α内的一个圆在平面β上的射影是离心率为 的椭圆,则角θ等于 .
的椭圆,则角θ等于 .
 的椭圆,则θ等于( )
的椭圆,则θ等于( )