Question

设数列{a_n}的前n项和为S_n,且(3-m)S_n+2ma_n=m+3(其中m为常数,n∈N₊),且m≠-3.

(1)求证:{a_n}为等比数列;

(2)若数列{a_n}的公比q=f(m),数列{b_n}满足b₁=a₁,b_n=f(b_n-1)(n∈N₊,n≥2),求证:{}为等差数列.

Answer 1

分析：本题要证数列为等差、等比数列,所以需按定义研究a_n+1与a_n的关系,而已知为S_n,需将S_n化为a_n,它们之间的关系为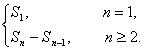

a_n=S₁,S_n-S_n-1,  n=1,n≥2.

证明：(1)由(3-m)S_n+2ma_n=m+3,得(3-m)S_n+1+2ma_n+1=m+3,

∴(3+m)a_n+1=2ma_n(m≠-3).

∴.

∴{a_n}为等比数列.

(2)由已知q=f(m)=,b₁=a₁=1,

∴当n≥2时,b_n=f(b_n-1)=·.

∴b_nb_n-1+3b_n=3b_n-1.

∴.

∴{}是首项为1、公差为的等差数列.

绿色通道

    证明数列为等差、等比数列需紧扣定义,找到a_n+1与a_n之间的关系,由已知前n项和S_n,求出a_n=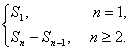由已知条件逐步变形得到,从而得证.