题目内容
(1)已知一元二次不等式ax2+bx+1>0的解集为{x|-2<x<1},求a+b的值.
(2)求函数y=2-x-
(x>0)的最大值,并指出此时x的值.
(2)求函数y=2-x-
| 9 | x |
分析:(1)由题意可得,二次函数y=ax2+bx+1的图象是开口向下的抛物线,且与x轴交于两点(-2,0),(1,0),再利用一元二次方程根与系数的关系求得a、b的值,可得a+b的值.
(2)由x+
≥6,可得y=2-(x+
)≤2-6,从而求得函数的最大值.
(2)由x+
| 9 |
| x |
| 9 |
| x |
解答:(1)解:由于不等式ax2+bx+1>0的解集为{x|-2<x<1},
所以二次函数y=ax2+bx+1的图象是开口向下的抛物线,…(1分)
且与x轴交于两点(-2,0),(1,0).…(2分)
所以-2和1是方程ax2+bx+1=0的两根,…(3分)
由此得
,…(4分) 解得a=b=-
.…(5分)
所以,a+b=-1.…(6分)
(2)解:因为x>0,所以x+
≥6,-(x+
)≤-6,…(8分)
当且仅当x=
即x=3时,等号成立.…(10分)
因此y=2-x-
≤2-6=-4,
即x=3时,函数取最大值-4.…(12分)
所以二次函数y=ax2+bx+1的图象是开口向下的抛物线,…(1分)
且与x轴交于两点(-2,0),(1,0).…(2分)
所以-2和1是方程ax2+bx+1=0的两根,…(3分)
由此得
|
| 1 |
| 2 |
所以,a+b=-1.…(6分)
(2)解:因为x>0,所以x+
| 9 |
| x |
| 9 |
| x |
当且仅当x=
| 9 |
| x |
因此y=2-x-
| 9 |
| x |
即x=3时,函数取最大值-4.…(12分)
点评:本题主要考查二次函数的性质应用,基本不等式的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
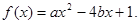 设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为
设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为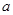 和
和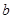 ,求函数
,求函数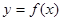 在区间[
在区间[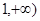 上是增函数的概率.
上是增函数的概率.