题目内容
设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率的取值范围是( )A.[-![]() ,
,![]() ] B.[-2,2] C.[-1,1] D.[-4,4]
] B.[-2,2] C.[-1,1] D.[-4,4]
解析:由题可知抛物线y2=8x的准线过(-2,0),
故过此点的直线l为:y=k(x+2).
将直线方程代入抛物线方程可得k2(x+2)2=8x,
化简得k2x2+(4k2-8)x+4k2=0有公共点,
即上述方程有解且解都大于或等于0.
当k=0时,x=0,成立;
当k≠0时,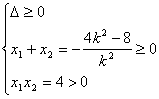
解得-1≤k≤1且k≠0.
综上所述,故-1≤k≤1.
答案:C

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率的取值范围是( )
A、[-
| ||||
| B、[-2,2] | ||||
| C、[-1,1] | ||||
| D、[-4,4] |
设抛物线y2=8x的焦点为F,过F,的直线交抛物线于A(x1,y1),B(x2,y2),则y1y2=( )
| A、8 | B、16 | C、-8 | D、-16 |