题目内容
在锐角三角形中,边a、b是方程x2-2
x+2=0的两根,角A、B满足:2sin(A+B)-
=0,求角C的度数,边c的长度及△ABC的面积.
| 3 |
| 3 |
由2sin(A+B)-
=0,得sin(A+B)=
,
∵△ABC为锐角三角形,
∴A+B=120°,C=60°.(4分)
又∵a、b是方程x2-2
x+2=0的两根,∴a+b=2
,a•b=2,(6分)
∴c2=a2+b2-2a•bcosC=(a+b)2-3ab=12-6=6,
∴c=
,(10分)
S△ABC=
absinC=
×2×
=
.(12分)
| 3 |
| ||
| 2 |
∵△ABC为锐角三角形,
∴A+B=120°,C=60°.(4分)
又∵a、b是方程x2-2
| 3 |
| 3 |
∴c2=a2+b2-2a•bcosC=(a+b)2-3ab=12-6=6,
∴c=
| 6 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |

练习册系列答案
相关题目
 x+2=0的两根,角A、B满足2sin(A+B)-
x+2=0的两根,角A、B满足2sin(A+B)-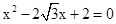 的两根,
的两根, ,求角C的度数,边c的长度及三角形ABO的面积
,求角C的度数,边c的长度及三角形ABO的面积