题目内容
已知函数f(x)=ax3+bx2+cx(a≠0,x∈R)为奇函数,且f(x)在x=1处取得极大值2.
(1)求函数y=f(x)的解析式;
(2)记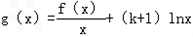 ,求函数y=g(x)的单调区间;
,求函数y=g(x)的单调区间;
(3)在(2)的条件下,当k=2时,若函数y=g(x)的图象在直线y=x+m的下方,求m的取值范围.
(1)求函数y=f(x)的解析式;
(2)记
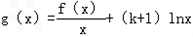 ,求函数y=g(x)的单调区间;
,求函数y=g(x)的单调区间;(3)在(2)的条件下,当k=2时,若函数y=g(x)的图象在直线y=x+m的下方,求m的取值范围.
解:(1)由f(x)=ax3+bx2+cx(a≠0)为奇函数,
∴f(﹣x)=﹣f(x),代入得,b=0
∴f'(x)=3ax2+c,且f(x)在x=1取得极大值2.
∴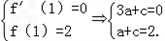
解得a=﹣1,c=3,
∴f(x)=﹣x3+3x
(2)∵g(x)=﹣x2+3+(k+1)lnx,
∴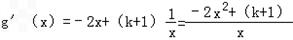
因为函数定义域为(0,+∞),
所以①当,k=﹣1时,g'(x)=﹣2x<0,函数在(0,+∞)上单调递减;
②当k<﹣1时,k+1<0,
∵x>0,
∴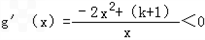 .可得函数在(0,+∞)上单调递减;
.可得函数在(0,+∞)上单调递减;
③k>﹣1时,k+1>0,
令g'(x)>0,得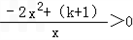 ,
,
∵x>0,
∴﹣2x2+(k+1)>0,得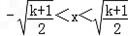 ,
,
结合x>0,得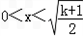 ;
;
令g'(x)<0,得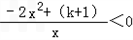 ,
,
同上得2x2>(k+1),解得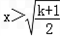 ,
,
∴k>﹣1时,单调递增区间为(0,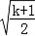 ),单调递增区间为(
),单调递增区间为(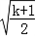 ,+∞)
,+∞)
综上,当k≤﹣1时,函数的单调递减区间为(0,+∞),无单调递增区间;
当k>﹣1时,函数的单调递增区间为(0,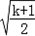 ),单调递减区间为(
),单调递减区间为(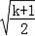 ,+∞)
,+∞)
(3)当k=2时,g(x)=﹣x2+3+3lnx,
令h(x)=g(x)﹣(x+m)=﹣x2﹣x+3lnx+3﹣m
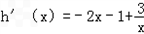 ,
,
令h'(x)=0,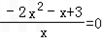 ,得x=1,
,得x=1,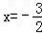 (舍去).
(舍去).
由函数y=h(x)定义域为(0,+∞),
则当0<x<1时,h'(x)>0,
当x>1时h'(x)<0,
∴当x=1时,函数h(x)取得最大值1﹣m.
由1﹣m<0得m>1
故m的取值范围是(1,+∞).
∴f(﹣x)=﹣f(x),代入得,b=0
∴f'(x)=3ax2+c,且f(x)在x=1取得极大值2.
∴
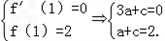
解得a=﹣1,c=3,
∴f(x)=﹣x3+3x
(2)∵g(x)=﹣x2+3+(k+1)lnx,
∴
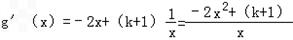
因为函数定义域为(0,+∞),
所以①当,k=﹣1时,g'(x)=﹣2x<0,函数在(0,+∞)上单调递减;
②当k<﹣1时,k+1<0,
∵x>0,
∴
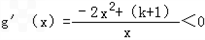 .可得函数在(0,+∞)上单调递减;
.可得函数在(0,+∞)上单调递减;③k>﹣1时,k+1>0,
令g'(x)>0,得
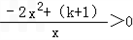 ,
,∵x>0,
∴﹣2x2+(k+1)>0,得
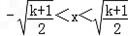 ,
,结合x>0,得
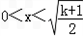 ;
;令g'(x)<0,得
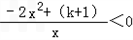 ,
,同上得2x2>(k+1),解得
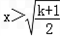 ,
,∴k>﹣1时,单调递增区间为(0,
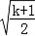 ),单调递增区间为(
),单调递增区间为(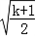 ,+∞)
,+∞)综上,当k≤﹣1时,函数的单调递减区间为(0,+∞),无单调递增区间;
当k>﹣1时,函数的单调递增区间为(0,
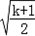 ),单调递减区间为(
),单调递减区间为(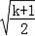 ,+∞)
,+∞)(3)当k=2时,g(x)=﹣x2+3+3lnx,
令h(x)=g(x)﹣(x+m)=﹣x2﹣x+3lnx+3﹣m
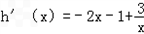 ,
,令h'(x)=0,
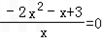 ,得x=1,
,得x=1,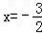 (舍去).
(舍去).由函数y=h(x)定义域为(0,+∞),
则当0<x<1时,h'(x)>0,
当x>1时h'(x)<0,
∴当x=1时,函数h(x)取得最大值1﹣m.
由1﹣m<0得m>1
故m的取值范围是(1,+∞).

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目