题目内容
已知定义在R上的函数f(x)=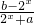 是奇函数
是奇函数
(1)求a,b的值;
(2)判断f(x)在R上的单调性并用定义证明.
解:(1)∵f(x)是定义在R上的奇函数,
∴f(0)= =0,解得b=1;
=0,解得b=1;
则f(x)= ,
,
因为f(-x)= =
= =-f(x)=
=-f(x)= ,
,
所以a•2x+1=a+2x,即a(2x-1)=2x-1对任意实数x都成立,
所以a=1,故a=b=1.
(2)f(x)= =
=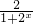 -1,f(x)在R上是减函数,
-1,f(x)在R上是减函数,
证明:任取x1,x2且x1<x2,
则f(x1)-f(x2)= -
- =
= ,
,
因为x10,
所以f(x1)-f(x2)>0,即f(x1)>f(x2),
故f(x)在R上是减函数.
分析:(1)由奇函数性质得f(0)=0,由此可求得b值;代入后由f(-x)=-f(x)恒成立可求得a值;
(2)任取x1,x2且x1<x2,通过作差可判断f(x1)与f(x2)大小关系,从而可知其单调性;
点评:本题考查函数奇偶性的性质及函数单调性的证明,属基础题,定义是解决该类问题的基本方法.
∴f(0)=
 =0,解得b=1;
=0,解得b=1;则f(x)=
 ,
,因为f(-x)=
 =
= =-f(x)=
=-f(x)= ,
,所以a•2x+1=a+2x,即a(2x-1)=2x-1对任意实数x都成立,
所以a=1,故a=b=1.
(2)f(x)=
 =
=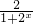 -1,f(x)在R上是减函数,
-1,f(x)在R上是减函数,证明:任取x1,x2且x1<x2,
则f(x1)-f(x2)=
 -
- =
= ,
,因为x10,
所以f(x1)-f(x2)>0,即f(x1)>f(x2),
故f(x)在R上是减函数.
分析:(1)由奇函数性质得f(0)=0,由此可求得b值;代入后由f(-x)=-f(x)恒成立可求得a值;
(2)任取x1,x2且x1<x2,通过作差可判断f(x1)与f(x2)大小关系,从而可知其单调性;
点评:本题考查函数奇偶性的性质及函数单调性的证明,属基础题,定义是解决该类问题的基本方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |