题目内容
7.若圆台两底面周长的比是1:4,过高的中点作平行于底面的平面,则圆台被分成两部分的体积比是( )| A. | 1:16 | B. | 39:129 | C. | 13:129 | D. | 3:27 |
分析 如图所示,不妨设圆台上底面为1,则下底面半径为4,中截面半径为r.设半径为1,r,4的3个圆锥的体积分别为V1,V2,V3.设PO1=h,OO1=OO2=x,由于O1A1∥OA∥O2A2,可得$\frac{h}{h+x}=\frac{1}{r}$,$\frac{h}{h+2x}=\frac{1}{4}$,解得r,x.再利用圆台的体积计算公式即可得出.
解答 解:如图所示,不妨设圆台上底面为1,则下底面半径为4,中截面半径为r.
设半径为1,r,4的3个圆锥的体积分别为V1,V2,V3.
设PO1=h,OO1=OO2=x,
∵O1A1∥OA∥O2A2,
∴$\frac{h}{h+x}=\frac{1}{r}$,$\frac{h}{h+2x}=\frac{1}{4}$,
解得$r=\frac{5}{2}$,x=$\frac{3}{2}h$.
∴V2-V1=$\frac{1}{3}×\frac{3}{2}h•[{1}^{2}+1×\frac{5}{2}+(\frac{5}{2})^{2}]$π=$\frac{39πh}{8}$,
V3-V2=$\frac{1}{3}×\frac{3h}{2}•π[(\frac{5}{2})^{2}+4×\frac{5}{2}+{4}^{2}]$=$\frac{129πh}{8}$,
∴圆台被分成两部分的体积比=39:129.
故选:B.
点评 本题考查了圆台的体积计算公式、平行线分线段成比例定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.在空间中,下列结论正确的是( )
| A. | 平行于同一直线的两直线平行 | B. | 垂直于同一直线的两直线平行 | ||
| C. | 平行于同一平面的两直线平行 | D. | 垂直于同一平面的两直线垂直 |
19.空间中,垂直于同一条直线的两条直线( )
| A. | 平行 | B. | 相交 | C. | 异面 | D. | 以上均有可能 |
17.已知圆C的圆心在y轴的负半轴上,且与x轴相切,被双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的渐近线截得的弦长为$\sqrt{3}$,则圆C的方程为( )
| A. | x2+(y+1)2=1 | B. | x2+(y+$\sqrt{3}$)2=3 | C. | x2+(y+$\frac{\sqrt{3}}{2}$)2=$\frac{3}{4}$ | D. | x2+(y+2)2=4 |

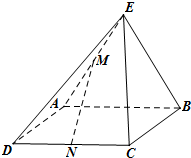 如图,矩形ABCD所在平面与直角三角形ABE所在平面互相垂直,AE⊥BE,点M,N分别是AE,CD的中点.
如图,矩形ABCD所在平面与直角三角形ABE所在平面互相垂直,AE⊥BE,点M,N分别是AE,CD的中点.