题目内容
已知y=logax,当x∈(3,+∞)时,总有|y|>1,则实数a的范围是( )
分析:当a>1时,不等式即 logax>1=logaa,故a<x对任意x∈(3,+∞)恒成立,得到1<a<3;当0<a<1时,有-logax=loga
>1=logaa,故a>
对任意x∈(3,+∞)恒成立,故
<a<1,将两种情况下求得的a的取值范围再取并集.
| 1 |
| x |
| 1 |
| x |
| 1 |
| 3 |
解答:解:当a>1时,
∵x∈[3,+∞),
∴y=f(x)=logax>0,
由|f(x)|>1,得logax>1=logaa,
∴a<x对任意x∈(3,+∞)恒成立.
于是:1<a<3;
当0<a<1时,
∵x∈(3,+∞),
∴y=f(x)=logax<0,
由|f(x)|>1,得-logax=loga
>1=logaa,
∴a<x对任意x∈(3,+∞)恒成立.
于是:
<a<1.
综之:a∈(
,1)∪(1,3).
故答案为:
<a<3且a≠1.
∵x∈[3,+∞),
∴y=f(x)=logax>0,
由|f(x)|>1,得logax>1=logaa,
∴a<x对任意x∈(3,+∞)恒成立.
于是:1<a<3;
当0<a<1时,
∵x∈(3,+∞),
∴y=f(x)=logax<0,
由|f(x)|>1,得-logax=loga
| 1 |
| x |
∴a<x对任意x∈(3,+∞)恒成立.
于是:
| 1 |
| 3 |
综之:a∈(
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查绝对值不等式的解法,对数函数的单调性及特殊点,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
有一段演绎推理是这样的:“因为对数函数y=logax是增函数;已知y=log
x是对数函数,所以y=log
x是增函数”的结论显然是错误的,这是因为( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、非以上错误 |








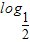 x是对数函数,所以y=
x是对数函数,所以y=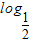 x是增函数”的结论显然是错误的,这是因为( )
x是增函数”的结论显然是错误的,这是因为( )