题目内容
如果函数f（x）=sin（2x+φ）+
cos（2x+φ）的图象关于原点对称，如果0≤φ≤π，那么?=（ ）
| 3 |
分析：利用三角函数的恒等变换化简函数f（x）的解析式为 2sin（2x+φ+
]，由题意可得 φ+
=kπ，k∈z，由此求得?的值．
| π |
| 3 |
| π |
| 3 |
解答：解：∵函数f（x）=sin（2x+φ）+
cos（2x+φ）=2[
sin（2x+φ）+
cos（2x+φ）]=2sin（2x+φ+
]，
由于它的图象关于原点对称，故函数f（x）为奇函数，故有 φ+
=kπ，k∈z．
再由 0≤φ≤π，可得 φ=
，
故选D．
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
由于它的图象关于原点对称，故函数f（x）为奇函数，故有 φ+
| π |
| 3 |
再由 0≤φ≤π，可得 φ=
| 2π |
| 3 |
故选D．
点评：本题主要考查三角函数的恒等变换及化简求值，由函数y=Asin（ωx+∅）的部分图象求解析式，属于中档题．
练习册系列答案
53随堂测系列答案
相关题目
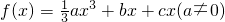，已知a＜b＜c，且
，曲线y=f（x）在x=1处取极值．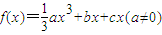
，已知a＜b＜c，且
，曲线y=f（x）在x=1处取极值．