题目内容
奇函数f（x）为[-1，1]上的减函数，解不等式f（a2）+f（2a）＞0．
解：由函数为奇函数可得f（-x）=-f（x）
∵函数f（x）[-1，1]上的减函数
由f（a2）+f（a）＞0可得，f（a2）＞-f（a）=f（-a）
∴
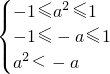
∴-1≤a≤0即不等式的解集{a|-1≤a≤0}
分析：由已知f（a2）+f（a）＞0结合函数为奇函数可得f（-x）=-f（x）及函数f（x）[-1，1]上的减函数可得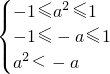解不等式可求
点评：本题主要考查了利用函数的奇函数的性质及函数的单调性解不等式，属于函数知识的综合应用．
∵函数f（x）[-1，1]上的减函数
由f（a2）+f（a）＞0可得，f（a2）＞-f（a）=f（-a）
∴
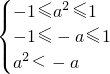
∴-1≤a≤0即不等式的解集{a|-1≤a≤0}
分析：由已知f（a2）+f（a）＞0结合函数为奇函数可得f（-x）=-f（x）及函数f（x）[-1，1]上的减函数可得
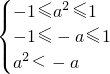解不等式可求点评：本题主要考查了利用函数的奇函数的性质及函数的单调性解不等式，属于函数知识的综合应用．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目