题目内容
设各项均为实数的等比数列{an}的前n项和为Sn,若S10=10,S30=70,则S40等于( )A.150
B.-200
C.150或-200
D.400或-50
【答案】分析:根据等比数列的前n项和的公式化简S10=10,S30=70,分别得到关于q的两个关系式,两者相除即可求出公比q的10次方的值,然后利用等比数列的前n项和的公式表示S40比S10的值,把q的10次方的值代入即可求出比值,根据比值即可得到S40的值.
解答:解:根据等比数列的前n项和的公式化简S10=10,S30=70得:
S10=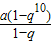 =10,S30=
=10,S30=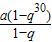 =70,
=70,
则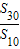 =
=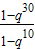 =
=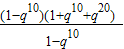 =7,得到1+q10+q20=7,
=7,得到1+q10+q20=7,
即(q10)2+q10-6=0,解得q10=-3(舍去),q10=2,
则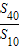 =
=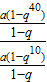 =
=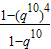 =
=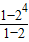 =15,
=15,
所以S40=15S10=150.
故选A
点评:此题考查学生灵活运用等比数列的前n项和的公式化简求值,是一道综合题.
解答:解:根据等比数列的前n项和的公式化简S10=10,S30=70得:
S10=
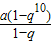 =10,S30=
=10,S30=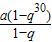 =70,
=70,则
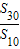 =
=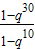 =
=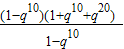 =7,得到1+q10+q20=7,
=7,得到1+q10+q20=7,即(q10)2+q10-6=0,解得q10=-3(舍去),q10=2,
则
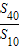 =
=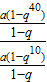 =
=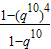 =
=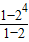 =15,
=15,所以S40=15S10=150.
故选A
点评:此题考查学生灵活运用等比数列的前n项和的公式化简求值,是一道综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的前四项和
的前四项和 ,且
,且 成等比.
成等比. 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值.
的最小值. 的前四项和
的前四项和 ,且
,且 成等比.
成等比. 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.