题目内容
设P：关于x的不等式ax＞1的解集是{x|x＜0}.Q：函数y=lg(ax2-x+a)的定义域为R.如果P和Q有且仅有一个正确,求a的取值范围.
思路分析：本题主要考查指数函数和对数函数的性质，在解此题时要分，P正确而Q不正确，Q正确而P不正确两种情况，然后分别求得a的范围.
解：使P正确的a的取值范围是0＜a＜1,
而Q正确
ax2-x+a对一切实数x恒大于0.
当a=0时,ax2-x+a=-x不能对一切实数恒大于0,
故Q正确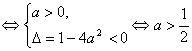
若P正确而Q不正确,则0＜a≤
；
若Q正确而P不正确,则a≥1.
故所求的a的取值范围是(0,
］∪［1,+∞).
练习册系列答案
相关题目