Question

如图2-2-3所示,四棱锥P—ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,且PB=4PM,PB与平面ABC成30°角.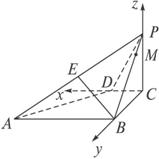

图2-2-3

(1)求证:CM∥平面PAD;

(2)求证:面PAB⊥面PAD.

Answer 1

证明:(1)以C为原点,以CD、CB、CP所在的直线分别为x、y、z轴建立空间直角坐标系.

∠PBC=30°,|PC|=2,|BC|=,|AB|=4,不难得出D(1,0,0),B(0,,0),P(0,0,2),M(0,).

设,y=.

∴共面.

∵CM平面PAD,∴CM∥平面PAD.

(2)作BE⊥PA于E,∵|PB|=|AB|=4,

∴E为PA中点.∴E(2,,1),则=(2,,1).

∴=0.

∴BE⊥DA.又BE⊥PA,

∴BE⊥面PAD.∴面PAB⊥面PAD.

    深化升华 在空间中证平行、垂直时,可建立空间直角坐标系,通过向量的坐标运算来证明问题,这是空间向量的一个重要应用.