题目内容
已知函数 .
.
(Ⅰ)若a=1,求函数f(x)的极值;
(Ⅱ)若函数f(x)在(1,2)上有极值,求a的取值范围.
解:(Ⅰ)函数f(x)的定义域为(0,+∞),
若a=1,则f(x)= -2x-3lnx.
-2x-3lnx.
f′(x)=x-2- =
= =
= .
.
当x∈(0,3)时,f′(x)<0;当x∈(3,+∞)时,f′(x)>0.
所以函数有极小值f(3)=- -3ln3,无极大值.
-3ln3,无极大值.
(II)f′(x)=ax-2+ =
= (x>0).
(x>0).
记h(x)=ax2-2x+a-4.
若f(x)在(1,2)上有极值,则h(x)=0有两个不等根且在(1,2)上有根.
由ax2-2x+a-4=0得a(x2+1)=2(x+2),
所以a= =
= .
.
令x+2=t,则t=x+2∈(3,4),y=t+ -4在(3,4)上递增,
-4在(3,4)上递增,
所以t+ -4∈(
-4∈( ,
, ),
), ,
,
故a∈( ,3),
,3),
经检验当a∈∈( ,3)时,方程h(x)=0无重根.
,3)时,方程h(x)=0无重根.
故函数f(x)在(1,2)上有极值时a的取值范围为( ,3).
,3).
分析:(Ⅰ)求出函数定义域,a=1时求出f′(x),在定义域内解不等式f′(x)>0,f′(x)<0,由导数符号即得函数f(x)的极值;
(Ⅱ)求导数f′(x)= (x>0),令h(x)=ax2-2x+a-4,则f(x)在(1,2)上有极值,等价于h(x)=ax2-2x+a-4=0有两个不等根且在(1,2)上有根.分离出参数a后,转化为求函数值域解决;
(x>0),令h(x)=ax2-2x+a-4,则f(x)在(1,2)上有极值,等价于h(x)=ax2-2x+a-4=0有两个不等根且在(1,2)上有根.分离出参数a后,转化为求函数值域解决;
点评:本题考查利用导数研究函数的极值及函数在某点取得极值的条件,解决(II)问的关键是对问题进行等价转化,变为方程根的分布问题加以解决.
若a=1,则f(x)=
 -2x-3lnx.
-2x-3lnx.f′(x)=x-2-
 =
= =
= .
.当x∈(0,3)时,f′(x)<0;当x∈(3,+∞)时,f′(x)>0.
所以函数有极小值f(3)=-
 -3ln3,无极大值.
-3ln3,无极大值.(II)f′(x)=ax-2+
 =
= (x>0).
(x>0).记h(x)=ax2-2x+a-4.
若f(x)在(1,2)上有极值,则h(x)=0有两个不等根且在(1,2)上有根.
由ax2-2x+a-4=0得a(x2+1)=2(x+2),
所以a=
 =
= .
.令x+2=t,则t=x+2∈(3,4),y=t+
 -4在(3,4)上递增,
-4在(3,4)上递增,所以t+
 -4∈(
-4∈( ,
, ),
), ,
,故a∈(
 ,3),
,3),经检验当a∈∈(
 ,3)时,方程h(x)=0无重根.
,3)时,方程h(x)=0无重根.故函数f(x)在(1,2)上有极值时a的取值范围为(
 ,3).
,3).分析:(Ⅰ)求出函数定义域,a=1时求出f′(x),在定义域内解不等式f′(x)>0,f′(x)<0,由导数符号即得函数f(x)的极值;
(Ⅱ)求导数f′(x)=
 (x>0),令h(x)=ax2-2x+a-4,则f(x)在(1,2)上有极值,等价于h(x)=ax2-2x+a-4=0有两个不等根且在(1,2)上有根.分离出参数a后,转化为求函数值域解决;
(x>0),令h(x)=ax2-2x+a-4,则f(x)在(1,2)上有极值,等价于h(x)=ax2-2x+a-4=0有两个不等根且在(1,2)上有根.分离出参数a后,转化为求函数值域解决;点评:本题考查利用导数研究函数的极值及函数在某点取得极值的条件,解决(II)问的关键是对问题进行等价转化,变为方程根的分布问题加以解决.

练习册系列答案
相关题目
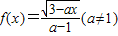 .
.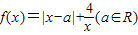 .
.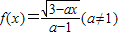 .
.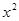 -ax-3(
-ax-3(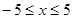 )
)