题目内容
下列函数中,在其定义域内既是增函数又是奇函数的是( )
分析:根据指数函数、对数函数、幂函数的图象和性质,及函数单调性的性质“增+增=增”,函数奇偶性的性质“奇+奇=奇”逐一判断四个答案是否满足条件,可得答案.
解答:解:函数y=
(x≠0)是奇函数,但在定义域内不是增函数,故A不满足条件;
函数y=-log2x在其定义域内增函数,但不是奇函数,故B不满足条件;
函数y=3x在其定义域内增函数,但不是奇函数,故C不满足条件;
函数y=x3,y=x均在其定义域内既是增函数又是奇函数,故函数y=x3+x在其定义域内既是增函数又是奇函数,故D满足条件
故选D
| 1 |
| x |
函数y=-log2x在其定义域内增函数,但不是奇函数,故B不满足条件;
函数y=3x在其定义域内增函数,但不是奇函数,故C不满足条件;
函数y=x3,y=x均在其定义域内既是增函数又是奇函数,故函数y=x3+x在其定义域内既是增函数又是奇函数,故D满足条件
故选D
点评:本题考查的知识点是函数奇偶性的判断,函数单调性的判断,是函数图象和性质的综合应用,熟练掌握基本初等函数的图象和性质是解答的关键.

练习册系列答案
相关题目
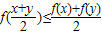 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数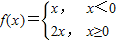
 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数