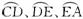题目内容
如图2-1-10，在Rt△ABC中，∠BCA=90°，以BC为直径的⊙O交AB于E点，D为AC的中点，连结BD交⊙O于F点.
图2-1-10
求证：
.
思路分析：要证
，虽然四条线段分别在△BEF与△BCF中，但这两个三角形一个是钝角三角形，另一个是直角三角形，不可能相似，故只能够借助中间比.
证明：连结CE，∵BC为⊙O的直径，∴∠BFC=90°，∠BEC=90°.
又∵∠ACB=90°，∴∠BCE=∠A.
又∵∠BFE=∠BCE,∴∠BFE=∠A.
∴△BEF∽△BAD.∴.
∵∠BFC=∠BCA，∠CBD=∠CBD,
∴△CBF∽△DBC.∴
.
又∵AD=CD，∴
.
练习册系列答案
快捷英语周周练系列答案
相关题目
.
上一动点(点P不与A、C重合),连结PC、PD、PA、AD,点E在AP的延长线上,PD与AB交于点F.给出下列四个结论:①CH2=AH·BH;②
=
;③AD2=DF·DP;④∠EPC=∠APD.
