题目内容
袋中装有若干个质地均匀大小相同的红球和白球,白球数量是红球数量的两倍.每次从袋中摸出一个球,然后放回.若累计3次摸到红球则停止摸球,否则继续摸球直至第5次摸球后结束.
(Ⅰ)求摸球3次就停止的事件发生的概率;
(Ⅱ)记摸到红球的次数为ξ,求随机变量ξ的分布列及其期望.
解:(Ⅰ)依题意,摸球1次,是红球的概率为 ,是白球的概率为
,是白球的概率为  .
.
摸球3次就停止,说明前3次分别都摸到了红球,则所求事件的概率为 P= =
= .
.
(Ⅱ) ξ 可能的取值为0,1,2,3.则 P(ξ=0 )= =
=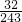 ,P( ξ=1)=
,P( ξ=1)=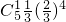 =
= ,
,
P(ξ=2)= =
= ,
,
P(ξ=3)=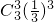 +
+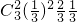 +
+ =
=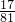 .
.
∴随机变量ξ的分布列是
ξ的数学期望为 Eξ=0×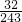 +1×
+1× +2×
+2× +3×
+3×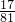 =
=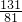 .
.
分析:(Ⅰ) 摸球3次就停止,说明前3次分别都摸到了红球,则所求事件的概率为 P= .
.
(Ⅱ) ξ 可能的取值为0,1,2,3,求出随机变量ξ取每个值的概率,即得分布列,从而求得期望.
点评:本题考查独立事件的概率,离散型随机变量的分布列,求出随机变量ξ取每个值的概率是解题的难点.
 ,是白球的概率为
,是白球的概率为  .
. 摸球3次就停止,说明前3次分别都摸到了红球,则所求事件的概率为 P=
 =
= .
. (Ⅱ) ξ 可能的取值为0,1,2,3.则 P(ξ=0 )=
 =
=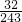 ,P( ξ=1)=
,P( ξ=1)=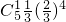 =
= ,
,P(ξ=2)=
 =
= ,
,P(ξ=3)=
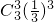 +
+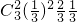 +
+ =
=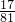 .
. ∴随机变量ξ的分布列是

ξ的数学期望为 Eξ=0×
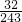 +1×
+1× +2×
+2× +3×
+3×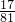 =
=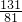 .
.分析:(Ⅰ) 摸球3次就停止,说明前3次分别都摸到了红球,则所求事件的概率为 P=
 .
.(Ⅱ) ξ 可能的取值为0,1,2,3,求出随机变量ξ取每个值的概率,即得分布列,从而求得期望.
点评:本题考查独立事件的概率,离散型随机变量的分布列,求出随机变量ξ取每个值的概率是解题的难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目