题目内容
设数列{an}的前n项和为Sn,且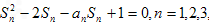 …
…
(1)求a1,a2;
(2)求证:数列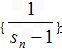 是等差数列,并求Sn的表达式.
是等差数列,并求Sn的表达式.
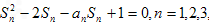 …
…(1)求a1,a2;
(2)求证:数列
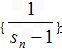 是等差数列,并求Sn的表达式.
是等差数列,并求Sn的表达式.(1)解:当n=1时,
由已知得
解得
同理,可解得
(2)证明 :由题设
当n≥2(n∈N*)时,an=Sn-Sn-1代入上式,得
∴
∴
∴
∴ 是首项为
是首项为 ,公差为-1的等差数列,
,公差为-1的等差数列,
∴
∴ 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
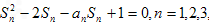 …
…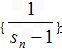 是等差数列,并求Sn的表达式.
是等差数列,并求Sn的表达式.(1)解:当n=1时,
由已知得
解得
同理,可解得
(2)证明 :由题设
当n≥2(n∈N*)时,an=Sn-Sn-1代入上式,得
∴
∴
∴
∴ 是首项为
是首项为 ,公差为-1的等差数列,
,公差为-1的等差数列,
∴
∴ 。
。

 阅读快车系列答案
阅读快车系列答案