题目内容
 如图,三角ABC是边长为4正三角形,PA⊥底面ABC,PA=
如图,三角ABC是边长为4正三角形,PA⊥底面ABC,PA=| 7 |
(1)证明:DE⊥平面PAC;
(2)求直线AD和平面PDE所成角的正弦值.
分析:(1)直接根据PA⊥底面ABC得到PA⊥DE;再结合DE⊥AC即可证明结论;
(2)方法一:先结合第一问的结论得到平面PDE⊥平面PAC;再点A作AF⊥PE,连接DF,根据条件推得∠ADF为直线AD和平面PDE所成角的平面角,最后在三角形中求出∠ADF解.
方法二:建立空间直角坐标系,求出直线的对应向量坐标,在求出平面的法向量的坐标,最后代入向量的夹角计算公式即可.
(2)方法一:先结合第一问的结论得到平面PDE⊥平面PAC;再点A作AF⊥PE,连接DF,根据条件推得∠ADF为直线AD和平面PDE所成角的平面角,最后在三角形中求出∠ADF解.
方法二:建立空间直角坐标系,求出直线的对应向量坐标,在求出平面的法向量的坐标,最后代入向量的夹角计算公式即可.
解答: 解:(1)∵PA⊥底面ABC,DE?底面ABC,
解:(1)∵PA⊥底面ABC,DE?底面ABC,
∴PA⊥DE,-------------------(2分)
又DE⊥AC,PA∩AC=A,
∴DE⊥平面PAC.------------------(4分)
(2)方法一:由(1)知,DE⊥平面PAC,又DE?平面PDE,
∴平面PDE⊥平面PAC.
过点A作AF⊥PE,连接DF.-------------------(6分)
∵平面PDE⊥平面PAC,平面PDE∩平面PAC=PE,AF?平面PAC,
∴AF⊥平面PDE,------(8分)
∴∠ADF为直线AD和平面PDE所成角的平面角.----------(10分)
∵△ABC是边长为4的正三角形,
∴AD=2
,AE=4-CE=4-
CD=3.
又∵PA=
,所以 PE=
=
=4,AF=
=
,
∴sin∠ADF=
=
.-------(13分)
即直线AD和平面PDE所成角的正弦值为
.-------------(14分)
方法二:如图所示,以点A为坐标原点,AD所在直线为x轴建立如图空间直角坐标系-----(2分)
∵在正三角形△ABC中,DE⊥AC,
∴AD=2
,AE=3,
∴A(0,0,0),P ( 0 , 0,
),D( 2
, 0 , 0 ),E (
,
,0 ).-----(6分)
易知
=( 2
, 0 , -
),
=(
,
, -
),
=( 2
,0 ,0 ).---(8分)
设 n=(x,y,z)是平面PDE的一个法向量,则
解得 x=
z,y=
z.
故可取 n=(
,
, 6 ).-------(11分)
于是cos<n ,
>=
=
=
.------(13分)
由此即知,直线AD和平面PDE所成角的正弦值为
.-----------(14分)
 解:(1)∵PA⊥底面ABC,DE?底面ABC,
解:(1)∵PA⊥底面ABC,DE?底面ABC,∴PA⊥DE,-------------------(2分)
又DE⊥AC,PA∩AC=A,
∴DE⊥平面PAC.------------------(4分)
(2)方法一:由(1)知,DE⊥平面PAC,又DE?平面PDE,
∴平面PDE⊥平面PAC.
过点A作AF⊥PE,连接DF.-------------------(6分)
∵平面PDE⊥平面PAC,平面PDE∩平面PAC=PE,AF?平面PAC,
∴AF⊥平面PDE,------(8分)
∴∠ADF为直线AD和平面PDE所成角的平面角.----------(10分)
∵△ABC是边长为4的正三角形,
∴AD=2
| 3 |
| 1 |
| 2 |
又∵PA=
| 7 |
| PA2+AE2 |
(
|
| AE•PA |
| PE |
3
| ||
| 4 |
∴sin∠ADF=
| AF |
| AD |
| ||
| 8 |
即直线AD和平面PDE所成角的正弦值为
| ||
| 8 |
方法二:如图所示,以点A为坐标原点,AD所在直线为x轴建立如图空间直角坐标系-----(2分)
∵在正三角形△ABC中,DE⊥AC,
∴AD=2
| 3 |
∴A(0,0,0),P ( 0 , 0,
| 7 |
| 3 |
3
| ||
| 2 |
| 3 |
| 2 |
易知
| PD |
| 3 |
| 7 |
| PE |
3
| ||
| 2 |
| 3 |
| 2 |
| 7 |
| AD |
| 3 |
设 n=(x,y,z)是平面PDE的一个法向量,则
|
解得 x=
| ||
| 6 |
| ||
| 6 |
故可取 n=(
| 21 |
| 7 |
于是cos<n ,
| AD |
n•
| ||
|n|•|
|
6
| ||
8×2
|
| ||
| 8 |
由此即知,直线AD和平面PDE所成角的正弦值为
| ||
| 8 |
点评:本题主要考察用空间向量求直线与平面的夹角以及直线与平面垂直的判定.一般在证明直线与平面垂直的判定问题时,常转化为证明线线垂直,进而得到直线与平面垂直.

练习册系列答案
相关题目
 如图,S是边长为a的正三角ABC所在平面外一点,SA=SB=SC=a,E、F是AB和SC的中点,则异面直线SA与EF所成的角为
如图,S是边长为a的正三角ABC所在平面外一点,SA=SB=SC=a,E、F是AB和SC的中点,则异面直线SA与EF所成的角为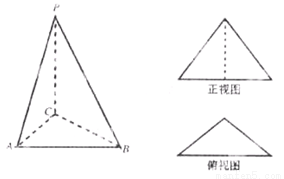
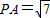 ,点D是BC的中点,点E在AC上,且DE⊥AC.
,点D是BC的中点,点E在AC上,且DE⊥AC.
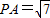 ,点D是BC的中点,点E在AC上,且DE⊥AC.
,点D是BC的中点,点E在AC上,且DE⊥AC.