题目内容
已知棱长为2的正方体
中,
分别是
的中点.
试求：(1)求
与
所成的角的余弦值的大小；
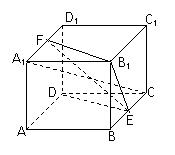(2)求
与平面
所成的角的正弦值的大小；
(3)求二面角
的大小的余弦值的大小.
解：建立空间坐标系,
为原点,
所在的直线分别为
轴,则有
(1)
,故与所成的角是
.-----5分
(2)
,平面的法向量n1
,
,故与平面所成的角是
.-----10分
(3)平面的法向量n1,平面
的法向量n2
,所
以
,故二面角的大小是
.-----15分.
练习册系列答案
相关题目
已知棱长为2的正方体的八个顶点都在同一个球面上，求这个球的体积（ ）
A、
| ||||
B、
| ||||
C、4
| ||||
| D、24π |
已知棱长为2的正方体的八个顶点都在同一个球面上，若在球内任取一点，则这一点q恰在正方体内的概率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|