Question

设函数f(x)=+lnx在［1,+∞)上为增函数.

(1)求正实数a的取值范围;

(2)若a=1,求证: +++…+＜lnn＜n++++…+(n∈N^*且n≥2).

Answer 1

(1)解:由已知,f′(x)=(a＞0),                                                               ?

依题意得≥0对x∈［1,+∞)恒成立,                                                         ?

∴ax-1≥0对x∈［1,+∞)恒成立.?

∴a-1≥0,即a≥1.                                                                                               ?

(2)证明:∵a=1,?

∴由(1)知,f(x)=+lnx在［1,+∞)上为增函数.?

∴当n≥2时,f()=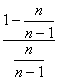+ln=ln-＞f(1)=0,?

即＜ln.                                                                                                       ?

∴+++…+＜ln+ln+…+ln=lnn.                                            ?

设g(x)=lnx-x,x∈［1,+∞)，则?

g′(x)= -1≤0对x∈［1,+∞)恒成立.?

∴g(x)在［1，+∞)上为减函数.                                                                         ?

∴n≥2时,g()=ln-＜g(1)=-1＜0.