Question

已知二次函数f（x）满足条件：f（0）=1，f（x+1）=f（x）+2x
（1）求f（x）
（2）讨论 f（|x|）=a（a∈R）的解的个数．

Answer 1

解：（1）设f（x）=ax²+bx+c（a≠0），∵f（0）=1，∴c=1．
∵f（x+1）=f（x）+2x，∴a（x+1）²+b（x+1）+1=ax²+bx+1+2x，
∴2ax+a+b≡2x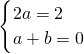，∴，解得，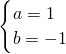
∴f（x）=x²-x+1．
（2）由f（|x|）=x²-|x|+1=，画出图象如图所示，
再画出函数y=a的图象，用虚线表示．
∵f（|x|）=，∴f（|x|）．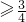
以下对a进行讨论．
当 a＜时，方程无解；
当a=或a＞1时，方程有两个解；
当a=1时方程有三个解；
当＜a＜1时，方程有四个解．
分析：（1）设出二次函数的解析式，根据条件f（0）=1，f（x+1）=f（x）+2x，即可求出a、b、c．
（2）根据解析式 f（|x|）画出图象，根据图象对a进行分类讨论即可．
点评：本题考查了利用二次函数的解析式和图象研究方程的根，根据二次函数的最小值和图象恰当的对a进行分类讨论是解决问题的关键．