��Ŀ����
����Ŀ�������ֻ��ķ�չ�����š�Խ��Խ��Ϊ���ǽ�����һ�ַ�ʽ.ij�����ԡ�ʹ���Ž�������̬�Ƚ��е��飬�����ȡ��50�ˣ����������Ƶ���ֲ����ԡ�ʹ���Ž��������������±�.
���䣨��λ���꣩ |
|
|
|
|
|
|
Ƶ�� | 5 | 10 | 15 | 10 | 5 | 5 |
������ | 5 | 10 | 12 | 7 | 2 | 1 |
�������ԡ����䡱45��Ϊ�ֽ�㣬������ͳ�������������![]() �����������ж��Ƿ���99%�İ�����Ϊ��ʹ���Ž�������̬�����˵������йأ�
�����������ж��Ƿ���99%�İ�����Ϊ��ʹ���Ž�������̬�����˵������йأ�
���䲻����45������� | �������45������� | �ϼ� | |
�� | |||
���� | |||
�ϼ� |
��������������![]() ��
��![]() �ı��������а��շֲ�����ķ���ѡȡ6�˽����ٵ��飬����������3�ˡ��������������3����������1��������
�ı��������а��շֲ�����ķ���ѡȡ6�˽����ٵ��飬����������3�ˡ��������������3����������1��������![]() �ĸ���.
�ĸ���.
�ο��������£�
���ٽ�ֵ����
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() �Ĺ۲�ֵ��
�Ĺ۲�ֵ�� 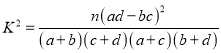 ������
������![]() ��
��
���𰸡���1����99%�İ��գ�2��![]()
�������������������1������������д����������Ϲ�ʽ��![]() �����ղο�����ȷ���Ƿ���99%�İ��գ�2���ȸ��ݷֲ����ȷ��
�����ղο�����ȷ���Ƿ���99%�İ��գ�2���ȸ��ݷֲ����ȷ��![]() ��ȡ2�ˣ�
��ȡ2�ˣ� ![]() ��ȡ4�ˣ�������ö�ٷ�ȷ����6������ȡ3���������������20�֣���������������1��������
��ȡ4�ˣ�������ö�ٷ�ȷ����6������ȡ3���������������20�֣���������������1��������![]() ���¼�����16������������ݹŵ�����ʹ�ʽ�����
���¼�����16������������ݹŵ�����ʹ�ʽ�����
������������⣺����������![]() ��������
��������
���䲻����45������� | �������45������� | �ϼ� | |
�� | 10 | 27 | 37 |
���� | 10 | 3 | 13 |
�� �� | 20 | 30 | 50 |
�������������������ݴ��빫ʽ�õ��� ![]()
������99%�İ�����Ϊ��ʹ���Ž�������̬�����˵������йأ�
���⣺���շֲ����������֪�� ![]() ��ȡ��
��ȡ�� ![]() ���ˣ���
���ˣ���
![]() ��ȡ��
��ȡ�� ![]() ���ˣ�
���ˣ�
��������ȡ��6���У�������![]() ��2�ˣ�����
��2�ˣ�����![]() ��4�ˣ�
��4�ˣ�
������![]() ��Ϊ
��Ϊ![]() ��������
��������![]() ��Ϊ
��Ϊ![]() �����6������ȡ3�����������Ϊ��
�����6������ȡ3�����������Ϊ�� ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��20�������
��20�������
����������һ��������![]() ������У�
������� ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����16�������
����16�������
��������һ��������![]() ��Ϊ�¼�
��Ϊ�¼�![]() ����
����![]()
��������һ��������![]() ��֮��ĸ���Ϊ
��֮��ĸ���Ϊ![]() ��
��





