题目内容
设函数的集合P={f(x)=log2(x+a)+b|a=-
,0,
,1;b=-1,0,1},
平面上点的集合Q={(x,y)|x=-
,0,
,1;y=-1,0,1},
则在同一直角坐标系中,P中函数f(x)的图象恰好经过Q中两个点的函数的个数是( )
| 1 |
| 2 |
| 1 |
| 2 |
平面上点的集合Q={(x,y)|x=-
| 1 |
| 2 |
| 1 |
| 2 |
则在同一直角坐标系中,P中函数f(x)的图象恰好经过Q中两个点的函数的个数是( )
| A、4 | B、6 | C、8 | D、10 |
分析:把P中a和b的值代入f(x)=log2(x+a)+b中,所得函数f(x)的图象恰好经过Q中两个点的函数的个数,即可得到选项.
解答:解:将数据代入验证知
当a=
,b=0;
a=
,b=1;
a=1,b=1
a=0,b=0
a=0,b=1
a=1,b=-1
时满足题意,
故选B.
当a=
| 1 |
| 2 |
a=
| 1 |
| 2 |
a=1,b=1
a=0,b=0
a=0,b=1
a=1,b=-1
时满足题意,
故选B.
点评:本题主要考查了函数的概念、定义域、值域、图象和对数函数的相关知识点,对数学素养有较高要求,体现了对能力的考查,属中档题

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
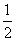 ,0,
,0,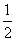 ,1;b=-1,0,1},平面上点的集合A={(x,y)|x=
,1;b=-1,0,1},平面上点的集合A={(x,y)|x=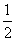 ,0,
,0,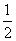 ,0,
,0,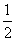 ,1;b=-1,0,1},平面上点的集合Q={(x,y)|x=-
,1;b=-1,0,1},平面上点的集合Q={(x,y)|x=-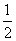 ,0,
,0,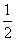 ,1;y=-1,0,1},则在同一直角坐标系中,P中函数f(x)的图象恰好经过Q中两个点的函数的个数是
,1;y=-1,0,1},则在同一直角坐标系中,P中函数f(x)的图象恰好经过Q中两个点的函数的个数是