题目内容
已知△ABC的三个顶点在抛物线 :x2=y上运动.
:x2=y上运动.(1)求
 的准线方程;
的准线方程;(2)已知点P的坐标为(2,6),F为抛物线
 的焦点,求|AP|+|AF|的最小值,并求此时A点的坐标;
的焦点,求|AP|+|AF|的最小值,并求此时A点的坐标;(3)若点A在坐标原点,BC边过定点N(0,1),点M在BC上,且
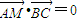 ,求点M的轨迹方程.
,求点M的轨迹方程.
【答案】分析:(1)由抛物线的方程,可得抛物线的焦点在y轴上,开口向上,故可得准线方程;
(2)利用抛物线的额窦炎,将点到焦点距离转化为到准线的距离,利用三点共线,即可得到结论;
(3)利用向量的垂直关系,即可求M的轨迹方程.
解答:解:(1)由x2=y得抛物线的焦点在y轴上,且2p=1,所以准线为y=- …(3分)
…(3分)
(2)解:由x2=y得抛物线的焦点在y轴上,且2p=1,所以,焦点坐标为(0, ) …(4分)
) …(4分)
由A作准线为y=- 的垂线,垂足为Q,当且仅当三点P,A,Q共线时,|AP|+|AF|取得最小,最小值为
的垂线,垂足为Q,当且仅当三点P,A,Q共线时,|AP|+|AF|取得最小,最小值为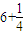 =
=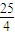 ,…(7分)
,…(7分)
此时A点的坐标为(2,4)…(9分)
(3)设点M的坐标为(x,y),BC边所在的方程过定点N(0,1),…(10分)
∴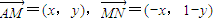
∵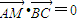
∴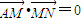 ,
,
所以,-x×x+y(1-y)=0,即y2+x2-y=0(x≠0)…(16分)
点评:本题考查抛物线的标准方程,考查抛物线的定义与性质,考查轨迹方程的求解,定位定量是关键.
(2)利用抛物线的额窦炎,将点到焦点距离转化为到准线的距离,利用三点共线,即可得到结论;
(3)利用向量的垂直关系,即可求M的轨迹方程.
解答:解:(1)由x2=y得抛物线的焦点在y轴上,且2p=1,所以准线为y=-
 …(3分)
…(3分)(2)解:由x2=y得抛物线的焦点在y轴上,且2p=1,所以,焦点坐标为(0,
 ) …(4分)
) …(4分)由A作准线为y=-
 的垂线,垂足为Q,当且仅当三点P,A,Q共线时,|AP|+|AF|取得最小,最小值为
的垂线,垂足为Q,当且仅当三点P,A,Q共线时,|AP|+|AF|取得最小,最小值为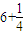 =
=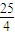 ,…(7分)
,…(7分)此时A点的坐标为(2,4)…(9分)
(3)设点M的坐标为(x,y),BC边所在的方程过定点N(0,1),…(10分)
∴
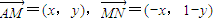
∵
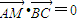
∴
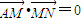 ,
,所以,-x×x+y(1-y)=0,即y2+x2-y=0(x≠0)…(16分)
点评:本题考查抛物线的标准方程,考查抛物线的定义与性质,考查轨迹方程的求解,定位定量是关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
已知△ABC的三个顶点在半径为1的球面上,且AB=1,BC=
.若A、C两点的球面距离为
,则球心O到平面ABC的距离为( )
| 3 |
| π |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|