题目内容
设f(x)的定义域为D,f(x)满足下面两个条件,则称f(x)为闭函数.
①f(x)在D内是单调函数;
②存在[a,b]⊆D,f(x)在[a,b]上的值域为[a,b].
如果f(x)= 为闭函数,那么k的取值范围是________.
为闭函数,那么k的取值范围是________.

分析:函数f(x)=
 是[
是[ ,+∞)上的增函数,因此若函数f(x)=
,+∞)上的增函数,因此若函数f(x)= 为闭函数,则可得函数y=f(x)的图象与直线y=x相交于点(a,a)和(b,b).因此方程k=x-
为闭函数,则可得函数y=f(x)的图象与直线y=x相交于点(a,a)和(b,b).因此方程k=x-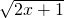 在[
在[ ,+∞)上有两个不相等的实数根a、b.最后采用换元法,讨论二次函数的单调性,可得f(x)=
,+∞)上有两个不相等的实数根a、b.最后采用换元法,讨论二次函数的单调性,可得f(x)= 为闭函数时,实数k的取值范围是:
为闭函数时,实数k的取值范围是: .
.解答:∵k是常数,函数y=
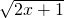 是定义在[
是定义在[ ,+∞)上的增函数,
,+∞)上的增函数,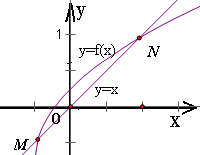
∴函数f(x)=
 是[
是[ ,+∞)上的增函数,
,+∞)上的增函数,因此,若函数f(x)=
 为闭函数,则存在区间[a,b]⊆D,
为闭函数,则存在区间[a,b]⊆D,使f(x)在[a,b]上的值域为[a,b].
可得函数y=f(x)的图象与直线y=x相交于点(a,a)和(b,b)(如图所示)
∴
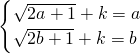 ,
,可得方程k=x-
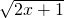 在[
在[ ,+∞)上有两个不相等的实数根a、b
,+∞)上有两个不相等的实数根a、b令t=
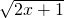 ,得x=
,得x= ,设函数F(x)═x-
,设函数F(x)═x-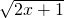 =g(t),(t≥0)
=g(t),(t≥0)即g(t)=
 t2-t-
t2-t- ,
,在t∈[0,1]时,g(t)为减函数-1≤g(t)≤
 ;在t∈[1,+∞)时,g(t)为增函数g(t)≥-1;
;在t∈[1,+∞)时,g(t)为增函数g(t)≥-1;∴当
 时,有两个不相等的t值使g(t)=k成立,相应地有两个不相等的实数根a、b满足方程k=x-
时,有两个不相等的t值使g(t)=k成立,相应地有两个不相等的实数根a、b满足方程k=x-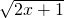 ,
,当f(x)=
 为闭函数时,实数k的取值范围是:
为闭函数时,实数k的取值范围是: .
.故答案为:

点评:本题以含有根式的函数为例,探求函数为闭函数时参数k的取值范围,着重考查了函数的单调性、换元法讨论二次函数等知识点,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目