题目内容
定义在R上的函数 满足:
满足: 的图像关于
的图像关于 轴对称,并且对任意的
轴对称,并且对任意的
 有
有 ,则当
,则当 时,有( )
时,有( )
A. | B. |
C. | D. |
A
解析试题分析:由已知,函数为偶函数,且在 是增函数,所以在(0,+
是增函数,所以在(0,+ )是减函数。而n+1>n>n-1,所以
)是减函数。而n+1>n>n-1,所以 即
即 ,选A。
,选A。
考点:本题主要考查函数的奇偶性、单调性。
点评:基础题,注意理解 是增函数的另一种表现形式。
是增函数的另一种表现形式。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数 的零点所在的区间是( )
的零点所在的区间是( )
A. | B. | C. | D. |
下列式子正确的是( )
A. | B. | C. | D. |
函数 的零点所在的一个区间是
的零点所在的一个区间是
A. | B. | C. | D. |
函数 的值域是( )
的值域是( )
A. | B. | C. | D. |
已知函数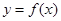 的周期为2,当
的周期为2,当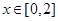 时,
时, ,如果
,如果
 ,则函数
,则函数 的所有零点之和为( )
的所有零点之和为( )
| A.2 | B.4 | C.6 | D.8 |
函数 和
和 的递增区间依次是( )
的递增区间依次是( )
A.(-∞,0 ,(-∞,1 ,(-∞,1 | B.(-∞,0 ,[1,+∞ ,[1,+∞ |
C.[0,+∞ ,(-∞,1 ,(-∞,1 | D.[0,+∞),[1,+∞) |
已知函数 ,若
,若 ,则
,则 等于 ( )
等于 ( )
A. | B. | C. | D. |
 其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=
其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=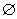 ,则f(P)∩f(M)=
,则f(P)∩f(M)=