Question

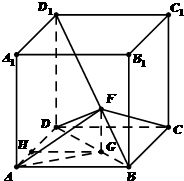已知长方体ADCD-A₁B₁C₁D₁，设动点F从B点出发，沿BD₁运动，G为F在底面ABCD的投影，AB=BC=2，AA₁=1，BF=x，
（1）求sin∠FBG，
（2）用x表示三棱锥G-ADF的体积V（x），当F在什么位置时，三棱锥G-ADF的体积V（x）最大，并求出最大体积．

Answer 1

分析：（1）根据长方体的结构特征，判断△BDD₁为直角三角形，求出对角线BD₁的长，可求sin∠FBG；
（2）过G作GH⊥AD，交AD于H，利用三角形的相似求出GH，再在△BFG中求FG，利用三棱锥的换底性求出体积关于x的函数，利用函数求最值的方法求解．

解答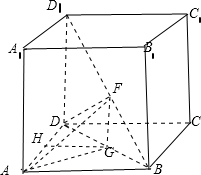：解：（1）在长方体ABCD-A₁B₁C₁D₁中BD1=

22+22+12

=3，sin∠FBG=

DD1

BD1

=

1

3

，
（2）过G作GH⊥AD，交AD于H，则GH∥AB，又FG⊥平面ABCD，∴FG∥DD₁，
∴

GH

AB

=

DG

DB

=

D1F

D1B

=

3-x

3

，∴GH=

2(3-x)

3

，
Rt△BFG中，FG=FB•sin∠FBG=x

DD1

BD1

=

x

3

，
S_△AGD=

1

2

×AD×GH=

2(3-x)

3

，（0＜x＜3）
V_G-ADF=V_F-ADG=

1

3

×

2(3-x)

3

×

x

3

=

6x-2x2

27

=

2

27

[-(x-

3

2

)2+

9

4

]，（0＜x＜3），
当x=

3

2

时，三棱锥G-ADF的体积V（x）体积最大，最大体积为

1

6

，

点评：本题考查棱柱的结构特征，棱锥的体积计算，考查了学生的空间想象能力，运算能力，利用三棱锥的换底性求出体积的函数关系式是解答本题的关键．