题目内容
设函数f(x)=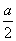 x2-1+cosx(a>0)。
x2-1+cosx(a>0)。
(1)当a=1时,证明; 函数y=f(x)在(0,+∞)上是增函数;
(2)若y=f(x)在(0,+∞)上是单调增函数,求正数a的范围;
(3)在(1)的条件下,设数列{an}满足:0<an<1,且an+1=f(an),求证:0<an+1<an<1。
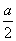 x2-1+cosx(a>0)。
x2-1+cosx(a>0)。 (1)当a=1时,证明; 函数y=f(x)在(0,+∞)上是增函数;
(2)若y=f(x)在(0,+∞)上是单调增函数,求正数a的范围;
(3)在(1)的条件下,设数列{an}满足:0<an<1,且an+1=f(an),求证:0<an+1<an<1。
解:(1)当a=1时, ,
,
 恒成立,
恒成立,
所以,y=g(x)在(0,+∞)上是增函数,所以 ,
,
∴函数y=f(x)在(0,+∞)上是增函数。
(2)若y=f(x)在(0,+∞)上是单调增函数,则 恒成立,
恒成立,
当 时,
时, ,恒有
,恒有 ,此时
,此时 ,
,
所以,y=f(x)在(0,+∞)上是单调增函数;
当 时,
时, ,得
,得 ,在
,在 上存在x0,使得
上存在x0,使得 ;
;
当 时,
时, ,
, ,
,
这与 ,
, 恒成立矛盾,所以,
恒成立矛盾,所以, 。
。
(3)由(1)当 时,
时, ;
;
当 假设
假设 ,则
,则 ,
,
所以, ,
,
又 ,
,
因为 ,
, ,
,
所以, ,即
,即 ,
,
所以, 。
。
 ,
, 恒成立,
恒成立,所以,y=g(x)在(0,+∞)上是增函数,所以
 ,
,∴函数y=f(x)在(0,+∞)上是增函数。
(2)若y=f(x)在(0,+∞)上是单调增函数,则
 恒成立,
恒成立,当
 时,
时, ,恒有
,恒有 ,此时
,此时 ,
,所以,y=f(x)在(0,+∞)上是单调增函数;
当
 时,
时, ,得
,得 ,在
,在 上存在x0,使得
上存在x0,使得 ;
;当
 时,
时, ,
, ,
,这与
 ,
, 恒成立矛盾,所以,
恒成立矛盾,所以, 。
。(3)由(1)当
 时,
时, ;
;当
 假设
假设 ,则
,则 ,
,所以,
 ,
,又
 ,
,因为
 ,
, ,
,所以,
 ,即
,即 ,
,所以,
 。
。 
练习册系列答案
相关题目
 设函数
设函数 设函数
设函数