题目内容
【题目】已知函数![]() ,
, ![]() ,
,![]() .
.
(Ⅰ)判断直线![]() 能否与曲线
能否与曲线![]() 相切,并说明理由;
相切,并说明理由;
(Ⅱ)若不等式![]() 有且仅有两个整数解,求
有且仅有两个整数解,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)假设直线与曲线相切,设出切点坐标![]() ,根据导数的几何意义,化简可得
,根据导数的几何意义,化简可得![]() ,根据切点既在曲线上又在切线上化简可得
,根据切点既在曲线上又在切线上化简可得![]() ,
,
两者联立消去![]() 将题意转化为
将题意转化为![]() ,令
,令![]() ,确定其在
,确定其在![]() 内有零点即可;(Ⅱ)将
内有零点即可;(Ⅱ)将![]() 转化为
转化为![]() ,令
,令![]() ,利用导数研究单调性证明
,利用导数研究单调性证明![]() 恒成立,分为
恒成立,分为![]() ,
, ![]() 不符合题意,当
不符合题意,当![]() 时,只需满足
时,只需满足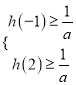 解出即可.
解出即可.
试题解析:(Ⅰ)假设存在这一的实数![]() 使得
使得![]() 的图象与
的图象与![]() 相切,设切点为
相切,设切点为![]() ,
,
由![]() 可知,
可知,![]() ,即
,即![]() ①
①
又函数![]() 的图象过定点(1,0),因此
的图象过定点(1,0),因此![]() ,即
,即![]() ②
②
联立①、②消去![]() 有
有![]() .
.
设![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
而![]() ,
,![]() ,
,![]() ,故存在
,故存在![]() ,使得
,使得![]() .
.
所以存在直线![]() 能与曲线
能与曲线![]() 相切.
相切.
(Ⅱ)由![]() 得
得![]() .
.
令![]() ,则
,则![]() .
.
令![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上有唯一零点,
上有唯一零点,![]() ,
,
此时![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
∴![]()
![]() ,
,
易证![]() ,
,![]()
![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)若![]() ,则
,则![]() ,此时
,此时![]() 有无穷多个整数解,不合题意;
有无穷多个整数解,不合题意;
(2)若![]() ,即
,即![]() ,因为
,因为![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() 时,
时,![]() ,所以
,所以![]() 无整数解,不合题意;
无整数解,不合题意;
(3)若![]() ,即
,即![]() ,此时
,此时![]() ,故0,1是
,故0,1是![]() 的两个整数解,
的两个整数解,
又![]() 只有两个整数解,因此
只有两个整数解,因此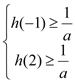 ,解得
,解得![]() .
.
所以![]() .
.

 千里马走向假期期末仿真试卷寒假系列答案
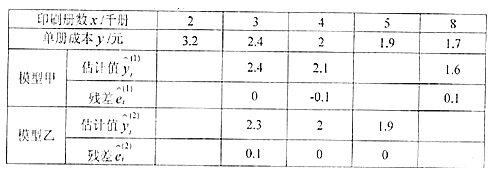
千里马走向假期期末仿真试卷寒假系列答案【题目】“中国式过马路”是网友对部分中国人集体闯红灯现象的一种调侃,即“凑够一撮人就可以走了,和红绿灯无关.”出现这种现象是大家受法不责众的“从众”心理影响,从而不顾及交通安全.某校对全校学生过马路方式进行调查,在所有参与调查的人中,“跟从别人闯红灯”“从不闯红灯”“带头闯红灯”人数如表所示:
跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 | |
男生 | 800 | 450 | 200 |
女生 | 100 | 150 | 300 |
(1)在所有参与调查的人中,用分层抽样的方法抽取n人,已知“跟从别人闯红灯”的人中抽取45人,求n的值;
(2)在“带头闯红灯”的人中,将男生的200人编号为1,2,…,200;将女生的300人编号为201,202,…,500,用系统抽样的方法抽取4人参加“文明交通”宣传活动,若抽取的第一个人的编号为100,把抽取的4人看成一个总体,从这4人中任选取2人,求这两人均是女生的概率.